
分析 (1)根据总量=速度×时间,可得函数关系;
(2)首先求得剩下的物资为150吨,可得解析式为t=$\frac{150}{v}$(v>0),再将t=2,代入解析式可得结果.
解答 解:(1)由已知得,vt=300.
∴t与v之间的函数关系式为t=$\frac{300}{v}$(v>0);
(2)运了一半物资后还剩:300×(1-$\frac{1}{2}$)=150(t),
故t与v之间的函数关系式变为t=$\frac{150}{v}$(v>0),
将t=2代入t=$\frac{150}{v}$,得2=$\frac{150}{v}$.
解得v=75.
因此剩下的物资要在2h之内运到江边,运输速度至少为75t/h.
点评 本题主要考查了反比例函数的应用,理清等量关系是解答此题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
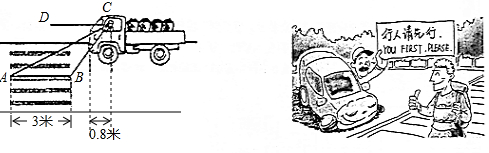
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
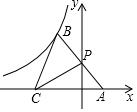 如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.
如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 方差 | C. | 中位数 | D. | 平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
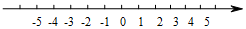 在数轴上表示下列各数,并用“<”连接起来.
在数轴上表示下列各数,并用“<”连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com