
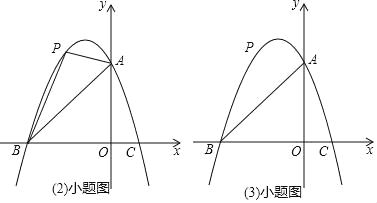
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпyЃНax2+bx+3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ1ЃЌ0ЃЉЃЌЕуPЪЧЯпЖЮABЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
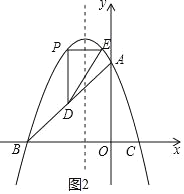
ЃЈ2ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїPABЕФУцЛ§зюДѓЃП
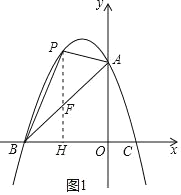
ЃЈ3ЃЉЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛЯпЖЮABгкЕуDЃЌдйЙ§ЕуPзїPEЁЮxжсНЛХзЮяЯпгкЕуEЃЌСЌНгDEЃЌЧыЮЪЪЧЗёДцдкЕуPЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3 ЃЈ2ЃЉЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ ЃЈ3ЃЉДцдкЃЌPЃЈЉ2ЃЌ3ЃЉЛђPЃЈ
ЃЉ ЃЈ3ЃЉДцдкЃЌPЃЈЉ2ЃЌ3ЃЉЛђPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃЛЃЈ2ЃЉЙ§ЕуPзїPHЁЭxжсгкЕуHЃЌНЛABгкЕуFЃЌжБЯпABНтЮіЪНЮЊyЃНx+3ЃЌЩшPЃЈtЃЌЉt2Љ2t+3ЃЉЃЈЉ3ЃМtЃМ0ЃЉЃЌдђFЃЈtЃЌt+3ЃЉЃЌдђPFЃНЉt2Љ2t+3ЉЃЈt+3ЃЉЃНЉt2Љ3tЃЌИљОнSЁїPABЃНSЁїPAF+SЁїPBFаДГіНтЮіЪНЃЌдйЧѓКЏЪ§зюДѓжЕЃЛЃЈ3ЃЉЩшPЃЈtЃЌЉt2Љ2t+3ЃЉЃЈЉ3ЃМtЃМ0ЃЉЃЌдђDЃЈtЃЌt+3ЃЉЃЌPDЃНЉt2Љ3tЃЌгЩХзЮяЯпyЃНЉx2Љ2x+3ЃНЉЃЈx+1ЃЉ2+4ЃЌгЩЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌPEЁЮxжсНЛХзЮяЯпгкЕуEЃЌЕУyEЃНyPЃЌМДЕуEЁЂPЙигкЖдГЦжсЖдГЦЃЌЫљвд![]() ЃНЉ1ЃЌЕУxEЃНЉ2ЉxPЃНЉ2ЉtЃЌЙЪPEЃН|xEЉxP|ЃН|Љ2Љ2t|ЃЌгЩЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯDPEЃН90ЁуЃЌЕУPDЃНPEЃЌдйЗжЧщПіЬжТлЃКЂйЕБЉ3ЃМtЁмЉ1ЪБЃЌPEЃНЉ2Љ2tЃЛЂкЕБЉ1ЃМtЃМ0ЪБЃЌPEЃН2+2t
ЃНЉ1ЃЌЕУxEЃНЉ2ЉxPЃНЉ2ЉtЃЌЙЪPEЃН|xEЉxP|ЃН|Љ2Љ2t|ЃЌгЩЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯDPEЃН90ЁуЃЌЕУPDЃНPEЃЌдйЗжЧщПіЬжТлЃКЂйЕБЉ3ЃМtЁмЉ1ЪБЃЌPEЃНЉ2Љ2tЃЛЂкЕБЉ1ЃМtЃМ0ЪБЃЌPEЃН2+2t
НтЃКЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+3Й§ЕуBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ1ЃЌ0ЃЉ
Ёр![]() НтЕУЃК
НтЕУЃК![]()
ЁрХзЮяЯпНтЮіЪНЮЊyЃНЉx2Љ2x+3
ЃЈ2ЃЉЙ§ЕуPзїPHЁЭxжсгкЕуHЃЌНЛABгкЕуF
ЁпxЃН0ЪБЃЌyЃНЉx2Љ2x+3ЃН3
ЁрAЃЈ0ЃЌ3ЃЉ
ЁржБЯпABНтЮіЪНЮЊyЃНx+3
ЁпЕуPдкЯпЖЮABЩЯЗНХзЮяЯпЩЯ
ЁрЩшPЃЈtЃЌЉt2Љ2t+3ЃЉЃЈЉ3ЃМtЃМ0ЃЉ
ЁрFЃЈtЃЌt+3ЃЉ
ЁрPFЃНЉt2Љ2t+3ЉЃЈt+3ЃЉЃНЉt2Љ3t
ЁрSЁїPABЃНSЁїPAF+SЁїPBFЃН![]() PFOH+
PFOH+![]() PFBHЃН
PFBHЃН![]() PFOBЃН
PFOBЃН![]() ЃЈЉt2Љ3tЃЉЃНЉ
ЃЈЉt2Љ3tЃЉЃНЉ![]() ЃЈt+
ЃЈt+![]() ЃЉ2+
ЃЉ2+![]()
ЁрЕуPдЫЖЏЕНзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁїPABУцЛ§зюДѓ
ЃЉЃЌЁїPABУцЛ§зюДѓ
ЃЈ3ЃЉДцдкЕуPЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮ
ЩшPЃЈtЃЌЉt2Љ2t+3ЃЉЃЈЉ3ЃМtЃМ0ЃЉЃЌдђDЃЈtЃЌt+3ЃЉ
ЁрPDЃНЉt2Љ2t+3ЉЃЈt+3ЃЉЃНЉt2Љ3t
ЁпХзЮяЯпyЃНЉx2Љ2x+3ЃНЉЃЈx+1ЃЉ2+4
ЁрЖдГЦжсЮЊжБЯпxЃНЉ1
ЁпPEЁЮxжсНЛХзЮяЯпгкЕуE
ЁрyEЃНyPЃЌМДЕуEЁЂPЙигкЖдГЦжсЖдГЦ
Ёр![]() ЃНЉ1
ЃНЉ1
ЁрxEЃНЉ2ЉxPЃНЉ2Љt
ЁрPEЃН|xEЉxP|ЃН|Љ2Љ2t|
ЁпЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯDPEЃН90Ёу
ЁрPDЃНPE
ЂйЕБЉ3ЃМtЁмЉ1ЪБЃЌPEЃНЉ2Љ2t
ЁрЉt2Љ3tЃНЉ2Љ2t
НтЕУЃКt1ЃН1ЃЈЩсШЅЃЉЃЌt2ЃНЉ2
ЁрPЃЈЉ2ЃЌ3ЃЉ
ЂкЕБЉ1ЃМtЃМ0ЪБЃЌPEЃН2+2t
ЁрЉt2Љ3tЃН2+2t
НтЕУЃКt1ЃН![]() ЃЌt2ЃН
ЃЌt2ЃН![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯЫљЪіЃЌЕуPзјБъЮЊЃЈЉ2ЃЌ3ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЪБЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЉЪБЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
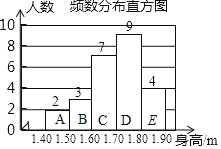
ЁОЬтФПЁПЮЊСЫНтбЇЩњЩэИпЃЌФГаЃЫцЛњГщШЁСЫ25ЮЛЭЌбЇЕФЩэИпЃЌАДееЩэИпЗжЮЊЃКAЃЌBЃЌCЃЌDЃЌEЮхИіаЁзщЃЌВЂЛцжЦСЫШчЯТЕФЭГМЦЭМЃЌЦфжаУПзщЪ§ОнОљАќКЌзюаЁжЕЃЌВЛАќКЌзюДѓжЕЃЎ
ЧыНсКЯЭГМЦЭМЃЌНтОіЯТСаЮЪЬтЃК
(1)етзщЪ§ОнЕФжаЮЛЪ§Тфдк_____зщЃЛ
(2)ИљОнИїаЁзщЕФзщжажЕЃЌЙРМЦИУаЃЭЌбЇЕФЦНОљЩэИпЃЛ
(3)аЁУїШЯЮЊдкЬт(2)ЕФМЦЫужаЃЌНЋDЃЌEСНзщЕФзщжажЕЗжБ№гУ1.70mКЭ1.90mНјааЬцЛЛЃЌВЂВЛгАЯьМЦЫуНсЙћЃЎЫћЕФЯыЗЈе§ШЗТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
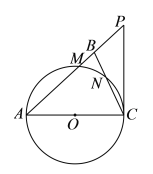
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABC=ЁЯACBЃЌвдACЮЊжБОЖЕФЁбOЗжБ№НЛABЁЂBCгкЕуMЁЂNЃЌЕуPдкABЕФбгГЄЯпЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпCPЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓжБОЖACЕФГЄМАЕуBЕНACЕФОрРыЃЎ
ЃЌЧѓжБОЖACЕФГЄМАЕуBЕНACЕФОрРыЃЎ
ЃЈ3ЃЉдкЕкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓ![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
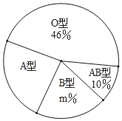
ЁОЬтФПЁПЁАжЛвЊШЫШЫЯзГівЛЕуАЎЃЌЪРНчНЋБфГЩУРКУЕФШЫМфЁБЃЎФГДѓбЇРћгУЁАЪРНчЯзбЊШеЁБПЊеЙзддИвхЮёЯзбЊЛюЖЏЃЌОЙ§МьВтЃЌЯзбЊепбЊаЭгаЁАAЁЂBЁЂABЁЂOЁБЫФжжРраЭЃЌЫцЛњГщШЁВПЗжЯзбЊНсЙћНјааЭГМЦЃЌИљОнНсЙћжЦзїСЫШчЭМСНЗљВЛЭъећЭГМЦЭМБэЃЈБэЃЌЭМЃЉЃК
бЊаЭЭГМЦБэ
бЊаЭ | A | B | AB | O |
ШЫЪ§ | ЁЁ ЁЁ | 10 | 5 | ЁЁ ЁЁ |
ЃЈ1ЃЉБОДЮЫцЛњГщШЁЯзбЊепШЫЪ§ЮЊЁЁ ЁЁШЫЃЌЭМжаmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋБэжаЕФЪ§ОнЃЛ
ЃЈ3ЃЉШєетДЮЛюЖЏжаИУаЃга1300ШЫвхЮёЯзбЊЃЌЙРМЦДѓдМгаЖрЩйШЫЪЧAаЭбЊЃП
ЃЈ4ЃЉЯжга4ИізддИЯзбЊепЃЌ2ШЫЮЊOаЭЃЌ1ШЫЮЊAаЭЃЌ1ШЫЮЊBаЭЃЌШєдк4ШЫжаЫцЛњЬєбЁ2ШЫЃЌРћгУЪїзДЭМЛђСаБэЗЈЧѓСНШЫбЊаЭОљЮЊOаЭЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁѕABCD жаЃЌЖдНЧЯп AC гы BD ЯрНЛгкЕу O ЃЌЕу E ЃЌ F ЗжБ№ЮЊ OB ЃЌ OD ЕФжаЕуЃЌбгГЄ AE жС G ЃЌЪЙ EG ЃНAE ЃЌСЌНг CG ЃЎ
ЃЈ1ЃЉЧѓжЄЃК ЁїABEЁеЁїCDF ЃЛ
ЃЈ2ЃЉЕБ AB гы AC ТњзуЪВУДЪ§СПЙиЯЕЪБЃЌЫФБпаЮ EGCF ЪЧОиаЮЃПЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2011ЩНЖЋМУФЯЃЌ27ЃЌ9ЗжЃЉШчЭМЃЌОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎХзЮяЯп![]() ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕуЃЈВЛгыЕуCжиКЯЃЉЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQ=CPЃЌСЌНгPQЃЌЩшCP=mЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіmЮЊКЮжЕЪБЃЌSШЁЕУзюДѓжЕЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯп![]() ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
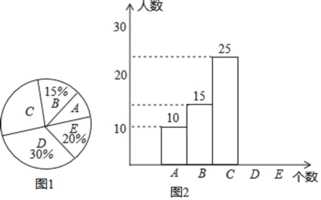
ЁОЬтФПЁПФГаЃОйааЁАККзжЬ§аДЁББШШќЃЌУПЮЛбЇЩњЬ§аДККзж39ИіЃЎБШШќНсЪјКѓЫцЛњГщВщВПЗжбЇЩњЬ§аДНсЙћЃЌЭМ1ЃЌЭМ2ЪЧИљОнГщВщНсЙћЛцжЦЕФЭГМЦЭМЕФвЛВПЗжЃЎ
зщБ№ | Ь§аДе§ШЗЕФИіЪ§x | ШЫЪ§ |
A | 0ЁмxЃМ8 | 10 |
B | 8ЁмxЃМ16 | 15 |
C | 16ЁмxЃМ24 | 25 |
D | 24ЁмxЃМ32 | m |
E | 32ЁмxЃМ40 | n |
ИљОнвдЩЯаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЙВЫцЛњГщВщСЫЖрЩйУћбЇЩњЃЌЧѓГіmЃЌnЕФжЕВЂВЙШЋЭМ2ЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓГіЭМ1жаЁЯІСЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИУаЃЙВга3000УћбЇЩњЃЌШчЙћЬ§аДе§ШЗЕФИіЪ§Щйгк24ИіЖЈЮЊВЛКЯИёЃЌЧыФуЙРМЦетЫљбЇаЃБОДЮБШШќЬ§аДВЛКЯИёЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁгБЭЌбЇдкЪжЙЄжЦзїжаЃЌАбвЛИіБпГЄЮЊ12cmЕФЕШБпШ§НЧаЮжНЦЌЬљЕНвЛИідВаЮЕФжНЦЌЩЯЃЌШєШ§НЧаЮЕФШ§ИіЖЅЕуЧЁКУЖМдкетИідВЩЯЃЌдђдВЕФАыОЖЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁНЋУПМўНјМлЮЊ80дЊЕФAЩЬЦЗАДУПМў100дЊГіЪлЃЌвЛЬьПЩЪлГі128МўЃЎОЙ§ЪаГЁЕїВщЃЌЗЂЯжетжжЩЬЦЗЕФЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌЦфШеЯњСППЩдіМг8МўЃЎЩшИУЩЬЦЗУПМўНЕМлxдЊЃЌЩЬГЁвЛЬьПЩЭЈЙ§AЩЬЦЗЛёРћШѓyдЊЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЈВЛБиаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЉ
ЃЈ2ЃЉAЩЬЦЗЯњЪлЕЅМлЮЊЖрЩйЪБЃЌИУЩЬГЁУПЬьЭЈЙ§AЩЬЦЗЫљЛёЕФРћШѓзюДѓЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com