
分析 由题意可知代数式的值即P(x,0)到A(0,a)和B(11,b)的距离之和,作出A关于x轴的对称点A′,显然当P为“x轴与线段A′B交点”时,PA+PB=A′B最短.
解答 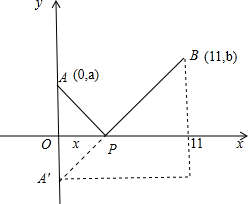 解:如图所示:设A(0,a),B(11,b),P点坐标为P(x,0),
解:如图所示:设A(0,a),B(11,b),P点坐标为P(x,0),
则PA=$\sqrt{{x}^{2}+{a}^{2}}$,PB=$\sqrt{(11-x)^{2}+{b}^{2}}$,
$\sqrt{{x^2}+{a^2}}+\sqrt{{{(11-x)}^2}+{b^2}}$的最小值就是PA+PB的最小值,
∵PA+PB的最小值为:$\sqrt{1{1}^{2}+(a+b)^{2}}$=$\sqrt{1{1}^{2}+{7}^{2}}$=$\sqrt{170}$,
∴代数式$\sqrt{{x^2}+{a^2}}+\sqrt{{{(11-x)}^2}+{b^2}}$的最小值为$\sqrt{170}$.
故答案为$\sqrt{170}$.
点评 本题考查了轴对称-最短路线问题,两点之间线段最短是解题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{27}=3\sqrt{3}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{5}×\sqrt{3}=\sqrt{15}$ | D. | $\sqrt{8}÷\sqrt{2}=2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将锐角△ABC绕点B逆时针旋转α(其中0°<α≤360°),得到△A′BC′,点D是边AB的中点,点P是边AC(含端点)上的一个动点,在△ABC绕点B逆时针旋转的过程中,点P的对应点是点P′.若AB=10,AC=8$\sqrt{2}$,∠ACB=45°,DP′的长度为x,则x的取值范围是7$\sqrt{2}$-5≤x≤19.
如图,将锐角△ABC绕点B逆时针旋转α(其中0°<α≤360°),得到△A′BC′,点D是边AB的中点,点P是边AC(含端点)上的一个动点,在△ABC绕点B逆时针旋转的过程中,点P的对应点是点P′.若AB=10,AC=8$\sqrt{2}$,∠ACB=45°,DP′的长度为x,则x的取值范围是7$\sqrt{2}$-5≤x≤19.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.
在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m≥3 | C. | m<3 | D. | m≤3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com