
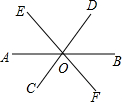
 直线AB,CD,EF相交于点O,如图.
直线AB,CD,EF相交于点O,如图.分析 (1)根据对顶角的定义即可解决问题.
(2)根据对顶角的性质即可解决问题.
(3)因为∠EOD=∠COF,所以∠BOE=∠BOD+∠EOD=∠BDO+∠COF,由此即可解决问题.
解答 解:(1)∠AOD的对顶角是∠BOC,∠EOC 的对顶角 ∠DOF,
∠DOF,
故答案为∠BOC,∠DOF.
(2)∵∠AOC=∠BOD(对顶角相等),
∵∠AOC=50°(已知),
∴∠BOD=50°(等量代换).
(3)∵∠BOE=∠EOD+∠BOD(角的和差定义),
又∵∠EOD=∠COF(对顶角相等),
∴∠BOE=∠BOD+∠COF=140°.
点评 本题考查对顶角的性质、邻补角的性质,解题的关键是灵活应用这些知识解决问题,属于基础题,中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 0 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a-3b)(3b-2a) | B. | (-2a+3b)(2a+3b) | C. | (-2a+3b)(2a-3b) | D. | (2a+3b)(-2a-3b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 120×10-9米 | B. | 1.2×10-7米 | C. | 1.20×10-6米 | D. | 12×10-4米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com