
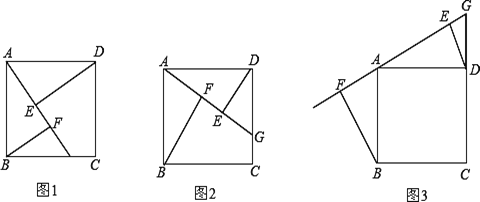
【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)
如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E.求证:△ABF≌△DAE;
(2) ①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E,线段EF与AF、BF的等量关系是______ ___;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,
线段EF与AF、BF的等量关系是______ ;
(3)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图并
探究线段EF与AF、BF的等量关系.
【答案】(1)详见解析;(2)① EF=BF-AF;②EF=AF+BF;(3)详见解析.
【解析】试题分析:(1) 利用正方形边相等和直角三角形角互余,证明△ABF和△DAE全等.
(2)画图,方法同(1)
(3)利用正方形的边的性质,证明△ABF和△DAE全等,
试题解析:
证明:(1)∵BF⊥AG,DE⊥AG
∴∠AFB=∠DEA=90°,
∵∠BAD=90°,
∴∠BAF=∠ADE(同角的余角相等),
∵四边形ABCD是正方形,
∴AB=AD,
在△ABF和△DAE中,
 ,
,
∴△ABF≌△DAE(AAS).
(2)①故答案为: EF=BF-AF,
② 故答案为:EF=AF+BF,
(3)如图4,
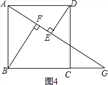
∵BF⊥AG,DE⊥AG,
∴∠AFB=∠DEA=90°,
∵∠BAD=90°,
∴∠BAF=∠ADE(同角的余角相等)
∵四边形ABCD是正方形,
∴AB=AD,
在△ABF和△DAE中
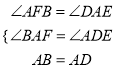 ,
,
∴△ABF≌△DAE(AAS),
∴AE=BF,
∴EF=AE-AF=BF-AF,
即EF=BF-AF.


科目:初中数学 来源: 题型:
【题目】唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云: 今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有.
注:古代一斗是10升.
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.
(1)列方程求壶中原有多少升酒;
(2)设壶中原有a0升酒,在第n个店饮酒后壶中余an升酒,如第一次饮后所余酒为a1=2a0﹣5(升),第二次饮后所余酒为a2=2a1﹣5=22a0﹣(22﹣1)×5(升),… 用含an﹣1的式子表示an= , 再用含a0和n的式子表示an=;
(3)按照这个约定,如果在第4个店喝光了壶中酒,请借助①中的结论求壶中原有多少升酒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB、CD相交于点O,OM⊥AB. 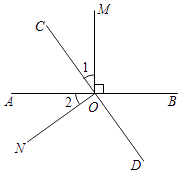
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1= ![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,直线AB、CD相交于点O,∠COE=90°. 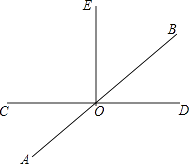
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一时刻,身髙1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得某旗杆的影长是5m,则该旗杆的高度是( )
A.1.25m
B.10m
C.20m
D.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )句.
①两条射线组成的图形叫做角;
②同角的补角相等;
③若AC=BC,则C为线段AB的中点;
④线段AB就是点A与点B之间的距离;
⑤平面上有三点A、B、C,过其中两点的直线有三条或一条.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com