练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列各数中，不是无理数的是（　　）
    A．$\sqrt{7}$B．$\frac{11}{7}$C．4πD．$\root{3}{9}$

    分析 根据无理数、有理数的定义即可判定选择项．

    解答 解：$\sqrt{7}$，4π，$\root{3}{9}$是无理数，
    $\frac{11}{7}$是有理数，
    故选：B．

    点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

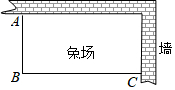    10．某家庭农场要建一个长方形的养兔场，兔场的两边靠墙（两堵墙互相垂直，长度不限），另两边用木栏围成，木栏总长20米．
    （1）兔场的面积能达到100平方米吗？请你给出设计方案；
    （2）兔场的面积能达到110平方米吗？如能，请给出设计方案，若不能说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

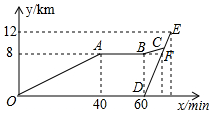    11．五一假期，小明骑自行车到松花江边游玩，从家出发40min后到达江边大塔，游玩一段时间后按原速度继续前往码头，在小明出发60min后，爸爸驱车沿相同路线前往码头，行驶8min时恰好经过江边大塔，如图是他们离开家的路程y（单位：km）关于小明离家时间x（单位：min）的函数图象．
    （1）小明骑车的速度为12km/h，点F的坐标是（68，8）；
    （2）小明从家出发多少分钟后被爸爸追上？
    （3）相遇后，爸爸载上小明和自行车同时到达码头（中间消耗时间忽略不计），求小明比预计时间早几分钟到达码头？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

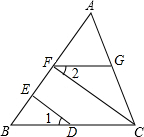    8．如图，CF⊥AB于F，DE⊥AB于E，∠1=∠2．求证：FG∥BC．
    证明：∵CF⊥AB，DE⊥AB
    ∴∠BED=90°，∠BFC=90° （垂直的定义）
    ∴∠BED=∠BFC
    ∴ED∥FC （同位角相等，两直线平行）
    ∴∠1=∠BCF （两直线平行，同位角相等）
    ∵∠2=∠1
    ∴∠2=∠BCF
    ∴FG∥BC （内错角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知直角三角形斜边长为（2$\sqrt{6}$+$\sqrt{3}$），一直角边长为（$\sqrt{6}$+2$\sqrt{3}$）．求这个直角三角形的另一直角边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，直线l1∥l2，直线l3和直线l1，l2分别交于点C和D，点P在CD上．
    （1）试找出∠1，∠2，∠3之间满足的数量关系，并说明理由；
    （2）如果点P在C，D两点之间运动时，∠1，∠2，∠3之间的关系是否会变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：如图所示，
    （1）画出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标．
    （2）在x轴上画出点P，使PA+PB最小（保留画图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）如图1，锐角△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE交于F，连DE，求证：DF•DA=DB•DC；
    （2）如图2，若∠BAC=90°，AD⊥BC于D，F为线段AD上一点，在AD延长线上找一点G使AD2=DF•DG，请画出图形找出点G并加以证明；
    （3）如图3，在（1）的条件下，若∠ABC=45°，EF=1，EC=3，直接写出BD长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．将抛物线y=-$\frac{1}{3}$x2+1向右平移1个单位再向上平移2个单位后所得到的抛物线的解析式为y=-$\frac{1}{3}$（x-1）2+3．

    查看答案和解析>>

    同步练习册答案