
【题目】在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴的负半轴相交于点C(如图),点C的坐标为(0,﹣3),且BO=CO.
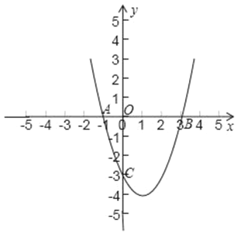
(1)求出B点坐标和这个二次函数的解析式;
(2)求△ABC的面积;
(3)设这个二次函数的图象的顶点为M,求AM的长.
【答案】(1)y=x2﹣2x﹣3;(2)S△ABC=6;(3)AM=2![]() .
.
【解析】
(1)首先根据BO=CO,可得B点的坐标为(3,0),然后把B,C点坐标分别代入解析式可得b,c的值,即可得解析式;
(2)令y=0,求出A点的坐标,即可根据图象求出△ABC的面积为![]() ×AB×OC;
×AB×OC;
(3)解析式化成顶点式,求得顶点M的坐标,过M作x轴的垂线MD,垂足为D,连接AM,则MD=4,AD=2,利用勾股定理即可求得AM的长.
(1)∵点C的坐标为(0,﹣3)
∴CO=|﹣3|=3
∵BO=CO
∴BO=3
∴B(3,0),
分别把B(3,0),C (0,﹣3)代入y=x2+bx+c,得![]() ,
,
解得![]()
∴二次函数的解析式为y=x2﹣2x﹣3;
(2)在y=x2﹣2x﹣3中,令y=0,得x2﹣2x﹣3=0
解得x1=﹣1,x2=3
∴AB=4,
∵点C的坐标为(0,﹣3)
∴CO=|﹣3|=3,
∴S△ABC =![]() ×AB×CO=
×AB×CO=![]() ×4×3=6;
×4×3=6;
(3)∵y=x2﹣2x﹣3=(x﹣1)2+4,
∴顶点M(1,﹣4),
过 M作x轴的垂线MD,垂足为D,连接AM,
则MD=4,AD=2,
∴AM=![]() =
=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
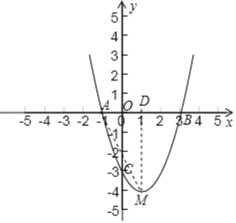
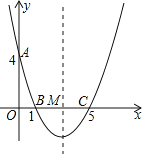
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
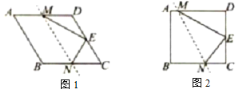
【题目】已知菱形纸片ABCD中,![]() ,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若
,点E是CD边的中点将该纸片折叠,使点B与点E重合,折痕交AD,BC边于点M,N,连接ME,NE.请从下面A,B两题中任选一题作答,我选择A.如图1,若![]() ,则ME的长为______;B.如图2,若
,则ME的长为______;B.如图2,若![]() ,则ME的长为_____.
,则ME的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A.图象分布在第一、三象限
B.当x>0时,y随x的增大而减小
C.图象经过点(2,3)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(a+1)x+a2+3=0有两个实数根x1,x2
(1)求实数a的取值范围
(2)若等腰△ABC的三边长分别为x1,x2,6,求△ABC的周长
(3)是否存在实数a,使x1,x2恰是一个边长为![]() 的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com