
【题目】七年级(2)班派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足的部分记为负数.评分记录如下:
+15,+20,-5,-4,-3,+4,+6,+2,+3,+5,+7,-8
(1)这12名同学中最高分和最低分各是多少分?
(2)超过基准分的有多少人?
(3)这12名同学的平均成绩是多少?
【答案】(1) 最高分是95分,最低分是67分; (2) 有8人;(3)78.5分.
【解析】试题分析:
(1)这12名学生的评分记录中最大的数和最小的数分别与75相加,所得的和就是最高分和最低分;
(2)评分记录为正的就是成绩超过基准分的人,数一数评分记录为正的有多少个人即可;
(3)求出12个评分记录的平均值再加上75所得即是这12名同学的平均成绩.
试题解析:
(1)观察评分记录可知:其中最大的数是+20,最小的是-8,
∴这12同学中最高分为:75+20=95(分);
最低分为:75+(-8)=67(分);
即这12名同学中竞赛得分最高分为95分,最低分为67分;
(2)∵12个评分记录中,正数有8个,
∴超过基准分的有8人;
(3)由题意可得这12名同学这次竞赛的平均成绩为:
![]()
=![]()
=![]() .
.
∴这12同学的平均成绩为78.5分.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列判断:
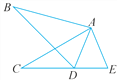
①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
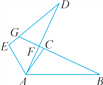
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
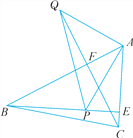
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
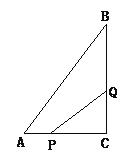
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com