
 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
分析 (1)根据扇形统计图中的数据可以得到机动车所占的百分比,本题得以解决;
(2)根据表格可以得到该年度重度污染和严重污染出现的频率共是多少;
(3)根据题意可得估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物.
解答 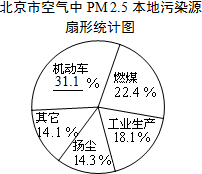 解:(1)由扇形统计图可得,
解:(1)由扇形统计图可得,
机动车为:1-22.4%-18.1%-14.3%-14.1%=31.1%,
故补全扇形统计图如右图所示,
(2)由表格可得,
该年度重度污染和严重污染出现的频率共是:$\frac{45+13}{41+135+84+47+45+13}$≈0.16,
即该年度重度污染和严重污染出现的频率共是0.16;
(3)由题意可得,
5200000×$\frac{40}{100}$×0.035=72800(千克)
即估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放72800千克污染物.
点评 本题考查扇形统计图、用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com