
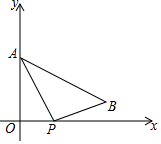
 如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:
如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:分析 ①利用勾股定理可以计算AB的长;
②如图2,作辅助线,利用面积差可得△APB的面积;
③如图3,分别以AB为腰和底边作等腰三角形有两个,以∠B为顶角,以AB为腰作等腰三角形,其另一点P交在x轴的负半轴上,这一种情况不成立;
④如图4,先作垂线段BD,由勾股定理可知:$\sqrt{9+{x}^{2}}$就是PA的长,$\sqrt{(4-x)^{2}+1}$就是PB的长,所以$\sqrt{9+{x}^{2}}$+$\sqrt{(4-x)^{2}+1}$的最小值就是PA+PB的最小值,根据轴对称的最短路径问题可得结论.
解答  解:①如图1,过B作BC⊥OA于C,
解:①如图1,过B作BC⊥OA于C,
∵点A(0,3)、点B(4,1),
∴AC=3-1=2,BC=4,
在Rt△ABC中,由勾股定理得:AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
故①结论不正确;
②如图2,在Rt△APO中,AO=3,AP=$\sqrt{13}$,
∴OP=$\sqrt{(\sqrt{13})^{2}-{3}^{2}}$=2,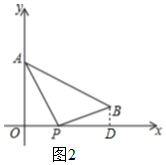
过B作BD⊥x轴于D,
∴BD=1,PD=4-2=2,
∴S△APB=S梯形AODB-S△AOP-S△PDB,
=$\frac{1}{2}$×OD×(BD+AO)-$\frac{1}{2}$AO•OP-$\frac{1}{2}$PD•BD,
=$\frac{1}{2}$×4×(1+3)-$\frac{1}{2}$×3×2-$\frac{1}{2}$×2×1,
=8-3-1,
=4,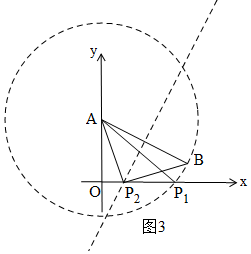
故②结论不正确;
③如图3,
i)以A为圆心,以AB为半径画圆与x轴的正半轴有一交点P1,得△AP1B是等腰三角形;
ii)作AB的中垂线,交x轴的正半轴有一交点P2,得△AP2B是等腰三角形;
综上所述,使△APB为等腰三角形的点P有2个;
故③结论不正确;
④如图4,过B作BD⊥x轴于D,
∵P(x,0),
∴OP=x,PD=4-x,
由勾股定理得:AP=$\sqrt{{3}^{2}+{x}^{2}}$=$\sqrt{9+{x}^{2}}$,PB=$\sqrt{(4-x)^{2}+1}$,
作A关于x轴的对称点A',连接A'B交x轴于P,则PA=PA',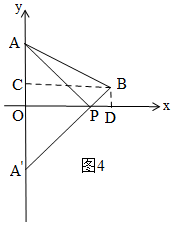
∴AP+PB=A'P+PB=A'B,
此时AP+PB的值最小,
过B作BC⊥OA于C,
则A'C=3+3-2=4,BC=4,
由勾股定理得:A'B=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴AP+PB的最小值是4$\sqrt{2}$,
即设点P的坐标为(x,0),则$\sqrt{9+{x}^{2}}$+$\sqrt{(4-x)^{2}+1}$的最小值为4$\sqrt{2}$.
故④结论正确;
综上所述,其中正确的结论有:④;
故答案为:④.
点评 本题考查了轴对称的最短路径问题、等腰三角形的判定、图形与坐标特点、勾股定理,是一个不错的综合题,难度适中,有等腰三角形和轴对称的作图问题,也有求最值问题,第4问中,熟练掌握并能灵活运用轴对称的最短路径问题是关键.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com