
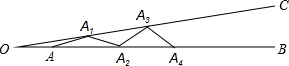
 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据等腰三角形的性质和三角形外角的性质依次可得∠A1AA2的度数,∠A2A1A3的度数,∠A3A2A4的度数,∠A4A3A5的度数,…,依此得到规律,再根据∠Ak+1AkAk+2<90°即可求解.
解答 解:由题意可知:AO=A1A,A1A=A2A1,…,
则∠AOA1=∠OA1A,∠A1AA2=∠A1A2A,…,
∵∠BOC=9°,
∴∠A1AA2=18°,∠A3A1A2=27°,∠A3A2A4=36°的度数,∠A4A3C=45°,…,
∴9°n<90°,
解得n<10.
∵n为整数,故n=9.
故选D.
点评 本题考查了等腰三角形的性质、三角形的一个外角等于和它不相邻的两个内角的和等知识,根据规律列出不等式是解题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
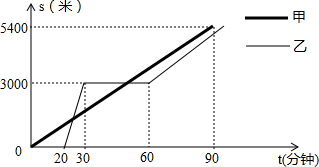 某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |
| B. |
| ||||||||||||||||||||||||||
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{11}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com