
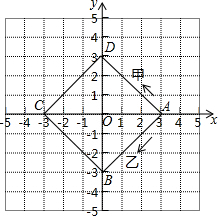
 如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (3,0) | B. | (-1,2) | C. | (-3,0) | D. | (-1,-2) |
分析 由甲、乙两物体单独环绕一周的时间即可算出两物体每两次相遇间的间隔时间,根据2017×8=24×672+8即可得出两个物体运动后的第2017次相遇地点为乙物体第8秒运动到的位置,结合图形找出乙物体第8秒运动到点的坐标即可得出结论.
解答 解:甲、乙两物体两次相遇间隔为1÷($\frac{1}{12}$+$\frac{1}{24}$)=8(秒),
∵2017×8=24×672+8,
∴两个物体运动后的第2017次相遇地点为乙物体第8秒运动到的位置.
∵乙物体第2秒运动到点(2,-1),乙物体第4秒运动到点(1,-2),乙物体第6秒运动到点(0,-3),乙物体第8秒运动到点(-1,-2),
∴两个物体运动后的第2017次相遇地点的坐标是(-1,-2).
故选D.
点评 本题考查了规律型中点的坐标,根据两物体的运动找出两物体第2017次相遇地点为乙物体第8秒运动到的位置是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
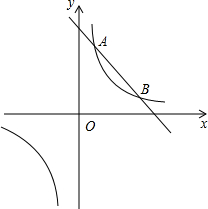 如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)
如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com