
【题目】如图等边![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() ,
,![]() 于
于![]() ,下列结论正确的是:________.①
,下列结论正确的是:________.①![]() 是
是![]() 中点;②
中点;②![]() ;③
;③![]() 是
是![]() 的切线;④
的切线;④![]() .
.
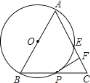
【答案】①②③④
【解析】
连接AP.根据圆周角定理、等腰三角形的“三线合一”的性质推知点P是线段BC的中点,同理证得点E是线段AC的中点;然后由三角形中位线定理,圆心角、弧、弦间的关系来证明![]() ;连接OP,由切线的判定证得OP⊥PF即可.
;连接OP,由切线的判定证得OP⊥PF即可.
连接AP.
∵AB是⊙O的直径,
∴∠APB=90°(直径所对的圆周角是直角),即AP⊥BC;
又∵AB=AC,
∴点P是线段BC的中点,
故①正确;
同理,点E是线段AC的中点,
∴AE=EC,
故④正确;
∵连接PE.
点P、E分别是线段BC、AC的中点,BC=AC=AB(等边三角形的三条边相等),
∴PE=![]() AB(三角形中位线定理),BP=
AB(三角形中位线定理),BP=![]() BC=
BC=![]() AB,
AB,
∴BP=PE(等量代换),
∴![]() ,
,
故②正确;
连接OP.
∵点P是线段BC的中点,点O是线段AB的中点,
∴OP是△ABC的中位线,
∴OP∥AC;
又∵PF⊥AC,
∴PF⊥OP,
∵点P在⊙O上,
∴PF是⊙O的切线;
故③正确.
综上所述,正确的结论有①②③④.
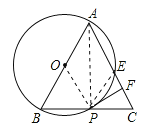
故答案为:①②③④.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,是由几个小立方块所搭几何体的俯视圈,小立方块中的数字表示在该位置小立方块的个数.
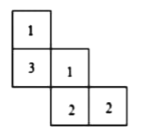
(1)请在网格内画出从正面和从左面看到的这个几何体的形状图.
(2)如图,是小明用9个棱长为1![]() 的小立方块积木搭成的几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数,他请小亮用尽可能少的同样大小的立方块在旁边再搭建一个几何体,使小亮所搭建的几何体恰好可以和小明所搭建的几何体拼成一个大的正方体(即拼大正方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
的小立方块积木搭成的几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数,他请小亮用尽可能少的同样大小的立方块在旁边再搭建一个几何体,使小亮所搭建的几何体恰好可以和小明所搭建的几何体拼成一个大的正方体(即拼大正方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
①小亮至少还需要 个小正方体;
②上面①中小亮所搭几何体的表面积为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
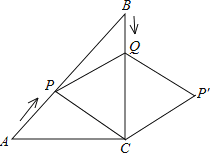
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.

(1)求证:CA2=CE CD;
(2)已知CA=5,EC=3,求sin∠EAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
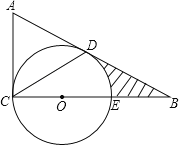
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,那么下列结论,①
,那么下列结论,①![]() 是等腰三角形;②
是等腰三角形;②![]() ;③若
;③若![]() ,
, ![]() ; ④
; ④![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
查看答案和解析>>
科目:初中数学 来源: 题型:
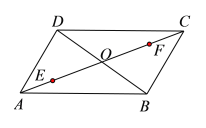
【题目】如图,已知平行四边形ABCD的对角线AC,BD相交于点O,AC=20 cm,BD=12 cm,两动点E,F同时以2 cm/s的速度分别从点A,C出发在线段AC上相对运动,点E到点C,点F到点A时停止运动.
(1)求证:当点E,F在运动过程中不与点O重合时,以点B,E,D,F为顶点的四边形为平行四边形;
(2)当点E,F的运动时间t为何值时,四边形BEDF为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
……
(1)按照此规律,写出第5个等式;
(2)按照此规律,写出第![]() (
(![]() 为正整数)个等式;
为正整数)个等式;
(3)利用(2)中写出的等式,求101+103+105+……+295+297+299的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com