
【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.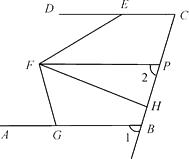
(1)说明:DC∥AB;
(2)求∠PFH的度数.
【答案】
(1)
∵ DC∥FP,
∴∠2=∠C.
∵ ∠1=∠2,
∴∠1=∠C,
∴DC∥AB.
(2)
∵ DC∥FP,DC∥AB,
∴∠PFE=∠FED=28,∠PFG=∠AGF=80,
∴∠EFG=∠PFE+∠PFG=28+80=108,
∵ FH平分∠EFG,
∴∠EFH=![]() ∠EFG=54,
∠EFG=54,
则∠PFH=∠EFH-∠PFE=54-28=26°.
【解析】(1)根据平行线的判定定理去判断;
(2)要求∠PFH,则要求∠EFH和∠PFE,根据平行线的性质可分别求出∠EFH和∠PFE.
【考点精析】通过灵活运用角的平分线和平行线的判定,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD

(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为4,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例:解方程![]()
解:设![]() ,则
,则![]() ,∴原方程可化为:
,∴原方程可化为:![]() ,解得
,解得![]()
当y=3时,![]() ,
,![]() ,当y=4时,
,当y=4时,![]() .
.
∴原方程有四个根是:![]() .
.
以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:![]() ;
;
(2)已知a、b、c是Rt△ABC的三边(c为斜边),![]() ,且a、b满足
,且a、b满足![]() ,试求Rt△ABC的周长.
,试求Rt△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AC上,DB=BC=AD,E是CD的中点,F是AB的中点,
(1)求证:EF=![]() AB.
AB.
(2) 当∠C=60 时, BC 、AB 与AC满足怎么样的关系?(直接写出答案,不必说明理由)
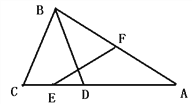
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.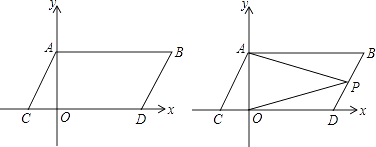
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合) ![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com