
分析 由非负数的性质可知:sinA=$\frac{\sqrt{2}}{2}$,cosB=$\frac{\sqrt{3}}{2}$,从而可求得∠A,∠B的度数,然后由三角形的内角和定理可求得∠C的度数.
解答 解:∵|sinA-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,
∴sinA=$\frac{\sqrt{2}}{2}$,cosB=$\frac{\sqrt{3}}{2}$.
∴∠A=45°,∠B=30°.
由三角形的内角和是180°可知∠C=180°-30°-45°=105°.
故答案为:105°.
点评 本题主要考查的是特殊锐角三角函数值、三角形的内角和定理、非负数的性质的应用,求得∠A,∠B的度数是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 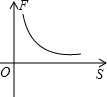 | C. |  | D. | 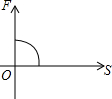 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
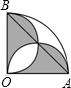 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )| A. | πcm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{1}{2}$cm2 | D. | $\frac{2}{3}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
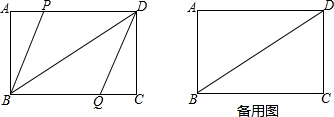
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com