练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

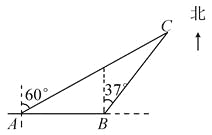
    【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发生了求救信号，一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里/时的速度前往救援，求海警船到达事故船C处所需的大约时间．(参考数据：sin53°≈0.8，cos53°≈0.6)

    【答案】（小时）.

    【解析】试题分析：作CD⊥AB于点D，根据Rt△ACD的三角函数求出CD的长度，然后根据Rt△CBD的三角函数求出BC的长度，然后根据时间=路程÷速度得出答案.

    试题解析：作CD⊥AB于点D，在Rt△ACD中，AC=80，∠CAB=30°， ∴CD=40(海里)，

    在Rt△CBD中，CB=≈=50(海里)，∴航行的时间t==1.25(h)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

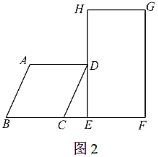
    【题目】小明在学完了平行四边形这个章节后，想对“四边形的不稳定性”和“四边形的判定”有更好的理解，做了如下的探究：他将8个木棍和一些钉子组成了一个正方形和平行四边形（如图1），且，在一条直线上，点落在边上．经小明测量，发现此时、、三个点在一条直线上，，．

    （1）求的长度；

    （2）设的长度为，________（用含的代数式表示）；

    （3）小明接着探究，在保证，位置不变的前提条件下，从点向右推动正方形，直到四边形刚好变为矩形时停止推动（如图2）．若此时，求的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，BC＝6，AB、AC的垂直平分线分别交边BC于点M、N，若MN＝2，则△AMN的周长是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

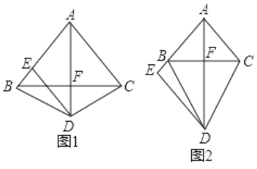
    【题目】如图1，已知△ABC中，AB=AC，点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC，过点D作DE//AC，交射线AB于E，连接AD交BC于F.

    (1)求证：AD垂直BC；

    (2)如图1，点E在线段AB上且不与B重合时，求证：DE=AE；

    (3)如图2，当点E在线段AB的延长线上时，请直接写出线段DE，AC，BE的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把的三边BA、CB和AC分别向外延长一倍，将得到的点，， 顺次连接成△，若△ABC的面积是3，则△的面积是（ ）

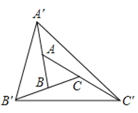
    A.15B.18C.21D.24

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是等边三角形，是边上的一点，连接，把绕着点逆时针旋转，得到，连接，若，，则的周长是（ ）

    A.16B.15C.13D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中的对角线AC，BD相交于O，EF过点O，与AD，BC分别相交于点E，F，若AB=4，BC=5，OE=1.5，则四边形EFCD的周长为（ ）

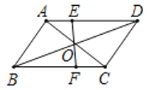
    A.10B.11C.12D.13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把一张矩形纸片ABCD按如图方式折叠，使点A与点E重合，点C与点F重合（E，F两点均在BD上），折痕分别为BH，DG．

    （1）求证：BH∥DG；

    （2）求证：△BEH≌△DFG；

    （3）若AB=6 cm，BC=8 cm．

    ①BF=________cm；

    ②求线段CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小莉的家在锦江河畔的电梯公寓AD内，她家的河对岸新建了一座大厦BC，为了测量大厦的高度，小莉在她家的楼底A处测得大厦顶部B的仰角为60°，爬上楼顶D处测得大厦顶部B的仰角为30°，已知电梯公寓高82米，请你帮助小莉计算出大厦的高度BC及大厦与电梯公寓间的距离AC．

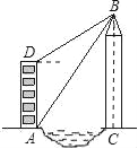
    查看答案和解析>>

    同步练习册答案