
分析 (1)利用网格特点和旋转的性质画出△A1B1C1,然后写出A1,B1,C1的坐标;
(2)用矩形的面积分别减去三个三角形的面积去计算出△A1B1C1的面积.
解答 解:(1)如图,△ABC绕原点顺时针方向旋转90°得到△A1B1C1,
点A1,B1,C1的坐标分别为(5,-1),(3,-2),(0,0);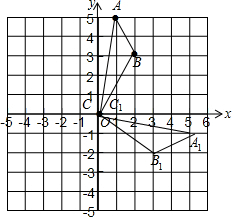
(2)△A1B1C1的面积=5×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×1×5=3.5.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )
二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )| A. | ①③ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
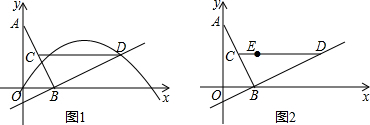
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k<0 | C. | k=0 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
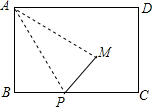 (背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究.
(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com