
【题目】现有五个小球,每个小球上面分别标着 1,2,3,4,5 这五个数字中的一个,这些小球除标的数字不同以外,其余的全部相同.把分别标有数字 4、5 的两个小球放入不透明的口袋 A 中,把分别标有数 字 1、2、3 的三个小球放入不透明的口袋 B 中.现随机从 A 和 B 两个口袋中各取出一个小球,把 从 A 口袋中取出的小球上标的数字记作 m,从B口袋中取出的小球上标的数字记作 n,且 m-n=k,则 y 关于 x 的二次函数 ![]() 与 x 轴有交点的概率是_________________.
与 x 轴有交点的概率是_________________.
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x+c交x轴于A、B两点(B在A左侧),交y轴于C,AB=10.
x+c交x轴于A、B两点(B在A左侧),交y轴于C,AB=10.
(1)求抛物线的解析式;
(2)在A点右侧的x轴上取点D,E为抛物线上第二象限内的点,连接DE交抛物线另外一点F,tan∠BDE=![]() ,DF=2EF,求E点坐标;
,DF=2EF,求E点坐标;
(3)在(2)的条件下,点G在x轴负半轴上,连接EG,EH∥AB交抛物线另外一点H,点K在第四象限的抛物线上,设DE交y轴于R,∠EHK=∠EGD+∠ORD,当HK=EG,求K点坐标.
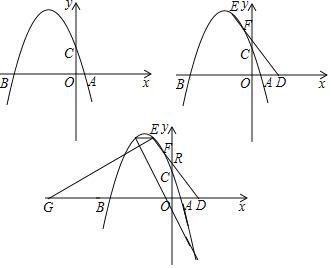
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A作射线交BE的延长线于点C,使∠EAC=∠EDA.
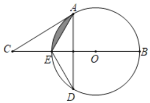
(1)求证:AC是⊙O的切线;
(2)若CE=AE=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级想了解初三年级1000名学生周末在家体育锻炼的情况,在初三年级随机抽取了20名男生和20名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:min):
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
统计数据,并制作了如下统计表:
时间 x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 | |
男生 | 2 | 8 | 8 | 2 | |
女生 | 1 | m | n | 3 |
分析数据:两组数据的极差、平均数、中位数、众数如下表所示
极差 | 平均数 | 中位数 | 众数 | |
男生 | a | 65.75 | b | 90 |
女生 | c | 75.5 | 75 | d |
(1)请将上面的表格补充完整:m= ,n= ,a= ,b= ,c= ,d=
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在 90min 以上的同学约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持李老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线p=ax2-10ax+8(a>0)经过点C、D,则点B的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,![]() 的三个顶点的分别为
的三个顶点的分别为![]() ,
,![]() ,
,![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).
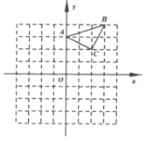
(1)在网格内画出![]() 向下平移2个单位长度得到的
向下平移2个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(2)以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(3)![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。
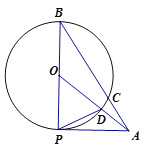
(1)求证:PO=PD
(2)若AC=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com