
����Ŀ�����壺��һ�������������y1��y2������xȡͬһ��ֵ��ʹ��y1��y2����ô��y1��y2Ϊ���������������ƶ�Ӧx��ֵΪy1��y2�ġ������㡱��
�����������������Ϊy1��y2Ϊ����������������ôy1+y2�����ֵ��Ϊy1��y2�ġ���Ӯֵ����
��1���жϺ���y��x+2m��y��![]() �Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
�Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
��2���жϺ���y��x+2m��y��3x��1��|x|��2���Ƿ�Ϊ������������������ǣ�����������㣻������ǣ���˵�����ɣ�
��3����֪����y��x+2m��y��x2����2m+1��x+��m2+4m��3����0��x��5���ǡ�����������������Ψһ�����㣮
�����m��ȡֵ��Χ��
�������ǵġ���Ӯֵ��Ϊ24�������m��ֵ��
���𰸡���1���� ���������������������㡱Ϊx��2��x����4����2������![]() ��m��
��m��![]() ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��
ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��![]() ��m����
��m����![]() ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ���������������3������3��m��1��2��m��6����m��2��
ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ���������������3������3��m��1��2��m��6����m��2��![]() ��m����3+
��m����3+![]() ��
��
��������
(1)����y��x+2m��y��![]() ��������һ���������ޣ��������������й����㣬�����ж����������ǡ�������������������x+2��
��������һ���������ޣ��������������й����㣬�����ж����������ǡ�������������������x+2��![]() �����x����4��x��2�����������㡱��
�����x����4��x��2�����������㡱��
(2)�����ǡ��������������������㡱Ϊx��m+![]() ������|x|��2���ɵõ���
������|x|��2���ɵõ���![]() ��m��
��m��![]() ʱ���ǡ���������������m��
ʱ���ǡ���������������m��![]() ��m����
��m����![]() ʱ�����ǡ�������������
ʱ�����ǡ�������������
(3)������֪�ɵã�x+2m��x2����2m+1��x+��m2+4m��3�������x��m+3��x��m��1��������֪�ɵõ�0��m+3��5ʱ����3��m��2����0��m��1��5ʱ��1��m��6����Ϊֻ��һ���������㡱��3��m��1��2��m��6����y��x+2m��0��x��5�����ֵΪ5+2m������3��m��1ʱ�������ĶԳ��ᩁ![]() ��m+
��m+![]() ��
��![]() ����ʱ��x��5ʱ�����ֵm2��6m+16����2��m��6ʱ���Գ���
����ʱ��x��5ʱ�����ֵm2��6m+16����2��m��6ʱ���Գ���![]() ��m+
��m+![]() ��
��![]() ����x��0ʱ�����ֵm2+4m��3�����ɡ���Ӯֵ��������mֵ��
����x��0ʱ�����ֵm2+4m��3�����ɡ���Ӯֵ��������mֵ��
�⣻(1)��y��x+2m�Ǿ�����һ����������ֱ�ߣ�y��![]() �Ǿ�����һ����������˫���ߣ�
�Ǿ�����һ����������˫���ߣ�
���������й����㣬
�����xȡͬһ��ֵ��ʹ��y1��y2��
�ຯ��y��x+2m��y��![]() �ǡ�������������
�ǡ�������������
��m��1ʱ��y��x+2��
��x+2��![]() �����x����4��x��2��
�����x����4��x��2��
�ࡰ�����㡱Ϊx��2��x����4��
(2)���躯��y��x+2m��y��3x��1�ǡ�������������
��x+2m��3x��1��
��x��m+![]() ��
��
��|x|��2��
�ੁ2��m+![]() ��2��
��2��
�ੁ![]() ��m��
��m��![]() ��
��
�൱��![]() ��m��
��m��![]() ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��
ʱ������y��x+2m��y��3x��1��|x|��2���ǡ���������������m��![]() ��m����
��m����![]() ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ�������������
ʱ������y��x+2m��y��3x��1��|x|��2�����ǡ�������������
(3)���ߺ���y��x+2m��y��x2����2m+1��x+��m2+4m��3����0��x��5���ǡ�������������
��x+2m��x2����2m+1��x+��m2+4m��3����
��x2����2m+2��x+��m2+2m��3����0��
��x��m+3��x��m��1��
��0��x��5ʱ��Ψһ�����㣬
��0��m+3��5ʱ����3��m��2��
��0��m��1��5ʱ��1��m��6��
�ੁ3��m��1��2��m��6ʱ���������⣻
��y��x+2m��0��x��5�����ֵΪ5+2m��
y��x2����2m+1��x+��m2+4m��3���ĶԳ���Ϊx��m+![]() ��
��
����3��m��1ʱ����![]() ��m+
��m+![]() ��
��![]() ��
��
��x��5ʱ�����ֵ�����ֵΪm2��6m+16��
��5+2m+m2��6m+17��24��
���m��2+![]() ��m��2��
��m��2��![]() ��
��
��m��2��![]() ��
��
��2��m��6ʱ����![]() ��m+
��m+![]() ��
��![]() ��
��
��x��0ʱ�����ֵ�����ֵΪm2+4m��3��
��5+2m+m2+4m��3��24��
���m����3+![]() ��m����3��
��m����3��![]() ��
��
��m����3+![]() ��
��
����������m��2��![]() ��m����3+
��m����3+![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�O�У���AC����BD������ΪH������BC������D��DE��BC�ڵ�E��DE��AC�ڵ�F��
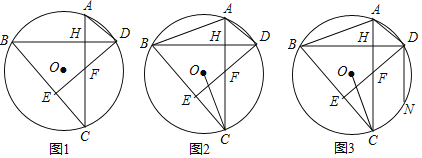
��1����ͼ1����֤��BDƽ�֡�ADF��
��2����ͼ2������OC����AC��BC����֤��OCƽ�֡�ACB��
��3����ͼ3���ڣ�2���������£�����AB������D��DN��AC����O�ڵ�N����AB��3![]() ��DN��9����sin��ADB��ֵ��
��DN��9����sin��ADB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ƭ�����˵�����Ϊ�������й��ƻ�Ƭ�Ĵ��ţ�2019Ҳ����Ϊ�й��ƻ�Ƭ��Ԫ�꣮ij��ӰԺΪ��ȫ���˽���ڶԡ����˵���������������������������飬��Ϊ�ĸ����A���dz����⣻B�����⣻C���������⣻D�������⣮���ݵ������ݻ��Ƴ�ͼ1��ͼ2��ͳ��ͼ����������������������Ϣ������������⣺

��1�����ν��ܵ���Ĺ��ڹ����� ���ˣ�
��2������ͳ��ͼ�У�����C��Բ�ĽǶ������� ����
��3���벹ȫ����ͳ��ͼ��
��4�������ڼ䣬�õ�ӰԺ���ۿ������˵��Ĺ���Լ3000�ˣ�����ƹ����жԸõ�Ӱ���⣨A��B��C����Ϊ���⣩��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x2��kx+k��2��0������ʵ����x1��x2����0��x1��1��2��x2��3����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
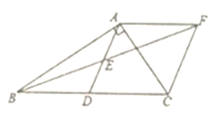
(1)��֤���ı���![]() �����Σ�
������
(2)��![]() ��
��![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x���ཻ��A(3��0)��B(1��0)���㣬��y���ཻ�ڵ�C(0��3)����C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��
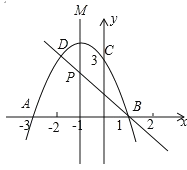
��1��D�����ꣻ
��2������κ����Ľ���ʽ��
��3������ͼ��ֱ��д��ʹһ�κ���ֵС�ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ��ף��ҵ�ٰ�����齱������ڿ�ҵ������깺��Ĺ˿ͣ����ܻ��һ�γ齱�Ļ��ᣬ�齱�������£���һ�������ĺ�����װ�зֱ��������1��2��3��3��С�����ǵ���״����С���ʵ���ȫ��ͬ���˿��ȴӺ��������ȡ��һ��С����С���ϱ��е����֣�Ȼ���С��Żغ��Ӳ�������ȣ��ٴӺ��������ȡ��һ��С����С���ϱ��е����֣����������μ��µ�����֮�ͣ����������õ�����֮��Ϊ6����ɻ��50Ԫ����ȯһ�ţ������õ�����֮��Ϊ5����ɻ��30Ԫ����ȯһ�ţ������õ�����֮��Ϊ4����ɻ��15Ԫ����ȯһ�ţ�������������н���
��1�������б�����״ͼ�ķ�����ѡ����һ�ּ��ɣ����ѳ齱һ�ο��ܳ��ֵĽ����ʾ������
��2��������μ��˸ó��п�ҵ�����һ�γ齱��������н��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
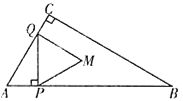
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������ÿ��2����λ���ٶ���
������ÿ��2����λ���ٶ���![]() ���յ�
���յ�![]() �˶�������
�˶�������![]() ��
��![]() �Ĵ��߽�����
�Ĵ��߽�����![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() �Ķ����غ�ʱ����
�Ķ����غ�ʱ����![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ��ʹ��
��ʹ��![]() �͵�
�͵�![]() ��ֱ��
��ֱ��![]() ��ͬ�࣬���
��ͬ�࣬���![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ���룩��
���룩��
��1����ȱ�������![]() �ı߳����ú�
�ı߳����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2������![]() ����
����![]() �ı�
�ı�![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() �غϲ���ͼ�ε����Ϊ
�غϲ���ͼ�ε����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��4����ֱ��![]() �����
�����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�ֱ�Ϊ
�ĶԳƵ�ֱ�Ϊ![]() ��ֱ��д��
��ֱ��д��![]() ʱ
ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com