
【题目】已知,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() 且
且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)在坐标轴上是否存在点![]() ,使三角形
,使三角形![]() 的面积是8?若存在,求出点
的面积是8?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)a=-4,b=2;(2)点C的坐标是(6,0)或(-2,0)或(0,4)或(0,-12)时,三角形![]() 的面积是8.
的面积是8.
【解析】
(1)根据绝对值的非负性和绝对值的非负性即可得到答案;
(2)由(1)得到点A、B的坐标,分两种情况设点C的坐标列方程求解即可.
(1)∵![]() ,
,
∴a+4=0,b-2=0
∴a=-4,b=2;
(2)存在,理由如下:
由(1)得到A(4,4),B(2,0),
分两种情况:
①当点C在x轴上时,设点C的坐标是(x,0),
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴![]() ,
,
解得x=6或-2,
∴C(6,0)或(-2,0);
②当点C在y轴上时,设点C的坐标是(0,y),
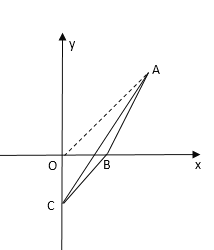
当点C在y轴正半轴上时,如图,连接OA,
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴![]() ,
,
解得y=4,
∴点C(0,4);
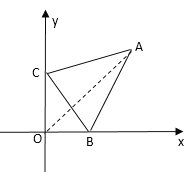
当点C在y轴负半轴上时,如图,连接OA,
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴ ![]() ,
,
∴![]() ,
,
解得y=-12或y=4(不合题意,舍去)
∴点C的坐标是(0,-12)
综上,点C的坐标是(6,0)或(-2,0)或(0,4)或(0,-12)时,三角形![]() 的面积是8.
的面积是8.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。

查看答案和解析>>
科目:初中数学 来源: 题型:
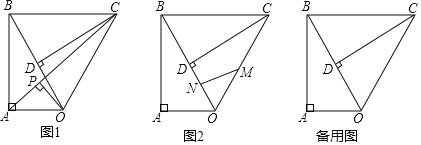
【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.
(1)填空:∠OBC= °;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
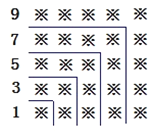
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com