
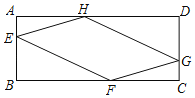
【题目】如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
【答案】(1)证明见解析;(2)四边形EFGH是平行四边形,理由见解析;(3)四边形EFGH的周长一半大于或者等于矩形ABCD一条对角线长度,理由见解析.
【解析】
(1)根据全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的性质得到:EH=GF,同理可得FE=HG,即可得四边形EFGH是平行四边形;
(3)由 轴对称--最短路径问题得到:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
解:(1)∵四边形ABCD是矩形,
∴![]() .
.
∴在![]() 与
与![]() 中,
中, ,
,
∴![]() ;
;
(2)∵由(1)知,![]() ,则
,则![]() ,同理证得
,同理证得![]() ,则
,则![]() ,
,
∴四边形EFGH是平行四边形;
(3) 四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.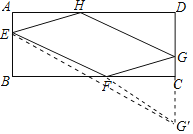
连接AC,
∵CG′=CG=AE,AB∥CG′,
∴四边形AEG′C为平行四边形,
∴EG′=AC.
在△EFG′中,∵EF+FG′≥EG′=AC,
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴相交于负半轴,给出五个结论:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤当﹣1<x<1时,y<0;其中正确的结论的序号( )
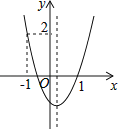
A.①③⑤B.②③④C.①③④D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:我们在学习四边形的相关知识时,认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形,下面我们用尺规作图的方法来体会它们之间的联系.如图,在□ABCD中,AB=4,BC=6,∠ABC=60°,请完成下列任务:
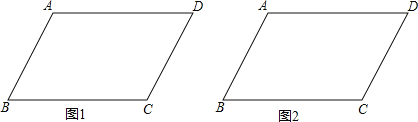
(1)在图1中作一个菱形,使得点A、B为所作菱形的2个顶点,另外2个顶点在□ABCD的边上;在图2中作一个菱形,使点B、D为所作菱形的2个顶点,另外2个顶点在□ABCD的边上;(尺规作图,保留作图痕迹,不写作法)
(2)请在图形下方横线处直接写出你按(1)中要求作出的菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
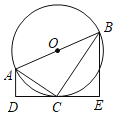
【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=![]() ,CE=3,则
,CE=3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() πC.
πC.![]() πD.
πD.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
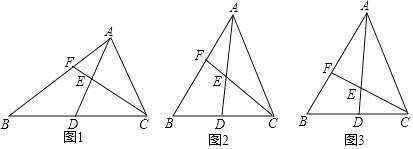
【题目】在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.
(1)尝试探究:如图1,当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是 ;
(2)类比延伸:如图2,当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)拓展迁移:如图3,当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△CDE都是等腰三角形,∠BAC=∠EDC=120°.
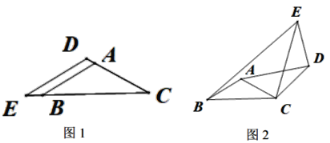
(1)如图1,A、D、C在同一直线上时,![]() =_______,
=_______,![]() =_______;
=_______;
(2)在图1的基础上,固定△ABC,将△CDE绕C旋转一定的角度α(0°<α<360°),如图2,连接AD、BE.
① ![]() 的值有没有改变?请说明理由.
的值有没有改变?请说明理由.
②拓展研究:若AB=1,DE=![]() ,当 B、D、E在同一直线上时,请计算线段AD的长;
,当 B、D、E在同一直线上时,请计算线段AD的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com