
【题目】小亮看到路边上有人设摊玩“有奖掷币”游戏,规则是交2元钱可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币都正面朝上,奖金5元;如果是其他情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).
(1)小亮应不应该玩?
(2)如果有100人,每人玩一次这种游戏,设摊者约获利多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
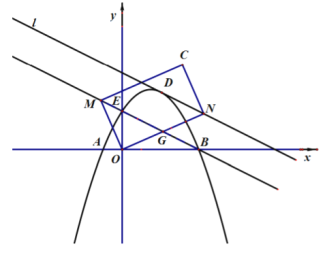
【题目】已知:如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 点和
点和![]() 点(
点(![]() 点在
点在![]() 点左则),交
点左则),交![]() 轴于
轴于![]() 点,作直线
点,作直线![]() 是直线
是直线![]() 上方抛物线上的一个动点.过
上方抛物线上的一个动点.过![]() 点作 直线
点作 直线![]() 平行于直线
平行于直线![]() 是直线
是直线 ![]() 上的任意点,
上的任意点,![]() 是直线
是直线![]() 上的任意点,连接
上的任意点,连接![]() ,始终保持
,始终保持![]() 为
为![]() ,以
,以![]() 和
和![]() 边,作矩形
边,作矩形![]() .
.
(1)在![]() 点移动过程中,求出当
点移动过程中,求出当![]() 的面积最大时点
的面积最大时点![]() 的坐标;在
的坐标;在![]() 的面积最大 时,求矩形
的面积最大 时,求矩形![]() 的面积的最小值.
的面积的最小值.
(2)在![]() 的面积最大时,线段
的面积最大时,线段![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 四个点组成平行 四边形时,求此时线段
四个点组成平行 四边形时,求此时线段![]() 与抛物线的交点坐标.
与抛物线的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
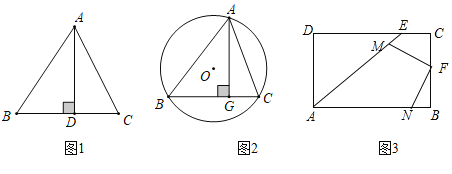
(1)如图1.在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() .则
.则![]() 面积的最大值是_______.
面积的最大值是_______.
(2)如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的外接圆,若
的外接圆,若![]() ,试判断
,试判断![]() 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
问题解决:
如图3,王老先生有一块矩形地![]() ,
,![]() ,
,![]() ,现在他想利用这块地建一个四边形鱼塘
,现在他想利用这块地建一个四边形鱼塘![]() ,且满足点
,且满足点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,这个四边形
,这个四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
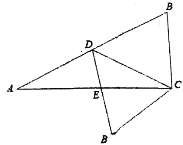
【题目】已知Rt△ABC,∠ACB=90,BC=10,AC=20,点D为斜边中点,连接CD,将△BCD沿CD翻折得△B’CD,B’D交AC于点E,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段路的“拥堵延时指数”计算公式为:拥堵延时指数=![]() ,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的
,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的![]() 倍,且A路段比B路段长1千米.
倍,且A路段比B路段长1千米.
(1)分别求平峰时A、B两路段的通行时间;
(2)第二季度大数据显示:在高峰时,A路段的拥堵延时指数为2,每分钟有150辆汽车进入该路段;B路段的拥堵延时指数为1.8,每分钟有125辆汽车进入该路段。第三季度,交管部门采用了智能红绿灯和潮汐车道的方式整治,拥堵状况有明显改善,在高峰时,A路段拥堵延时指数下降了a%,每分钟进入该路段的车辆增加了![]() ;B路段拥堵延时指数下降
;B路段拥堵延时指数下降![]() ,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多
,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多![]() 小时,求a的值.
小时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
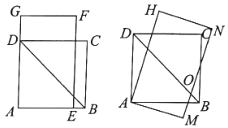
【题目】如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,长方形
的正方形,长方形![]() 的宽
的宽![]() ,长
,长![]() .将长方形
.将长方形![]() 绕点
绕点![]() 顺时针旋转15°得到长方形
顺时针旋转15°得到长方形![]() (如图所示),这时
(如图所示),这时![]() 与
与![]() 相交于点
相交于点![]() .则在图中,
.则在图中,![]() ,
,![]() 两点间的距离是( )
两点间的距离是( )
A.![]() B.5C.
B.5C.![]() D.7
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com