
分析 将两等式左右两边相减,左边整理后分解因式,根据1-ab2≠0的题设条件求得b2=-a,代入所求的分式化简,再将a2=-2a+1代入,整理后即可求出值.
解答 解:∵a2+2a-1=0,b4-2b2-1=0,
∴(a2+2a-1)-(b4-2b2-1)=0,
化简之后得到:(a+b2)(a-b2+2)=0,
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0,
因此a+b2=0,即b2=-a,
又因为a2+2a-1=0,即a2=-2a+1,
则($\frac{ab^2+b^2+1}{a}$)2012
=$(\frac{-{a}^{2}-a-2a+1}{a})^{2012}$
=$(\frac{2a-1-a-2a+1}{a})^{2012}$
=(-1)2012
=1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8.
如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
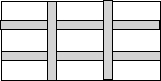 如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?
如图,资江风光带有一块长100米,宽50米的草坪,要在中间铺设两横两纵且宽度一样的小路,若草坪面积恰好3600平方米,求小路的宽为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com