
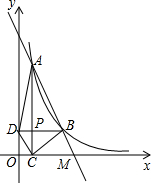
 如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.
如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.分析 (1)把A点坐标代入反比例函数解析式可求得k的值;
(2)由平行线分线段成比例可求得AP与AC的比例,从而可求得B点的坐标,则可求得BD的长,利用三角形面积公式可求得△ABD的面积;
(3)由菱形的性质可用B点坐标表示出P点坐标,再结合PA=PC可求得m、n的值,即可求得B点坐标,利用待定系数法可求得直线AB的解析式.
解答 解:
(1)把A(1,8)代入y=$\frac{k}{x}$,可得k=8;
(2)∵A(1,8),B(m,n),
∴AP=8-n,AC=8,
∵AB=2BM,
∴$\frac{AB}{AM}$=$\frac{2}{3}$,
∵AC⊥x轴,BD⊥y轴,
∴BP∥CM,
∴$\frac{AP}{AC}$=$\frac{AB}{AM}$=$\frac{2}{3}$,即$\frac{8-n}{8}$=$\frac{2}{3}$,解得n=$\frac{8}{3}$,
把B(m,$\frac{8}{3}$)代入反比例函数解析式可得m=3,
∴BD=3,
∴S△ABD=$\frac{1}{2}$BD•AP=$\frac{1}{2}$×3×(8-$\frac{8}{3}$)=8;
(3)∵四边形ABCD为菱形,
∴BP=DP,
∴点P坐标为($\frac{1}{2}$m,n),
∵PA=PC,
∴P(1,4),
∴$\frac{1}{2}$m=1,n=4,
∴m=2,n=4,
∴B(2,4),
设直线AB解析式为y=sx+b,
∴$\left\{\begin{array}{l}{4=2k+b}\\{8=k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-4}\\{b=12}\end{array}\right.$,
∴直线AB的解析式为y=-4x+12.
点评 本题为反比例函数的综合应用,涉及待定系数法、平行线分线段成比例、菱形的性质、方程思想等知识.在(1)中注意待定系数法的应用,在(2)、(3)中求得B点坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
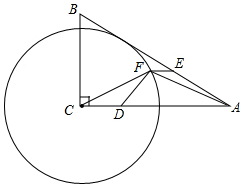 如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13×103千克 | B. | 1.3×103千克 | C. | 1.3×104千克 | D. | 1.3×105千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中xOy中,抛物线y=$\frac{1}{2}$x2-mx+$\frac{1}{2}$m2+m-2的顶点在x轴上.
在平面直角坐标系中xOy中,抛物线y=$\frac{1}{2}$x2-mx+$\frac{1}{2}$m2+m-2的顶点在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
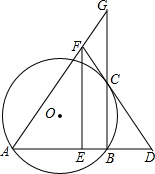 如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF∥BC交DC的延长线于点F,连接AF并延长BC的延长线于点G
如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF∥BC交DC的延长线于点F,连接AF并延长BC的延长线于点G查看答案和解析>>
科目:初中数学 来源: 题型:选择题
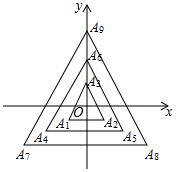 如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )
如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )| A. | (0,448) | B. | (-672,$224\sqrt{3}$) | C. | (0,$448\sqrt{3}$) | D. | (0,$224\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com