
【题目】如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.

【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() ;(3)①5;② P1(2.5,0),P2(9-
;(3)①5;② P1(2.5,0),P2(9-![]() ,0),P3(
,0),P3(![]() ,0).
,0).
【解析】
(1)由抛物线过原点和点A(10,0)设其解析式为![]() ,代入点B的坐标(2,2)解得a的值即可得到抛物线的解析式;
,代入点B的坐标(2,2)解得a的值即可得到抛物线的解析式;
(2)由已知条件求出直线AB的解析式,由点P的坐标为(m,0)结合已知条件可得OQ=10-2m,由此即可用含m的式子表达出DQ的长度,这样由四边形ACDE是正方形即可由S=![]() DQ2求出S与m之间的函数关系式了;
DQ2求出S与m之间的函数关系式了;
(3)①将x=2代入抛物线解析式得y=2,可知点N的坐标为(2,2),点G的坐标为(2,4),当GF和EQ落在同一条直线上时,△FGQ为等腰直角三角形,则PQ=PG=4,OQ=OP+PQ=6,将x=6代入直线AB解析式可求得得点M的坐标为(6,1),即QM=1,由旋转法可知,每一个阴影部分面积等所在正方形面积的一半,由此可求两个阴影部分面积和;②分为PF、DE在同一直线上;PF、CQ在同一直线上;GF、CD在同一直线上三种情况分析计算求出相应的P点的坐标即可.
(1)∵抛物线过O(0,0),A(10,0),
∴设抛物线解析式为![]() ,
,
将B(2,2)代入,得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() ,
,
即 :![]() ;
;
(2)设直线AB的解析式为:![]() ,将A(10,0),B(2,2)代入,得
,将A(10,0),B(2,2)代入,得![]() ,解得
,解得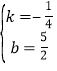 ,
,
∴![]() ,
,
∵P(m,0),
∴OP=m,AQ=2m,OQ=10-2m,
∴当x=10-2m时,QM=![]() ,
,
∴QD=m,
∵四边形QCDE是正方形,
∴![]() ;
;
(3)① ∵点P的坐标为(2,0),
∴将x=2代入抛物线解析式:![]() 可得点N的坐标为(2,2),
可得点N的坐标为(2,2),
由正方形的性质可得点G的坐标为:(2,4),
∴PG=4,
又∵当GF和EQ落在同一条直线上时,△PGQ为等腰直角三角形,
∴PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式![]() 可得点M的坐标为:(6,1),即QM=1,QD=2,
可得点M的坐标为:(6,1),即QM=1,QD=2,
∴阴影部分面积和=![]() ×(
×(![]() PG2+
PG2+![]() QD2)=5;
QD2)=5;
②若点P继续向点A运动,则当两个正方形分别有边落在同一条直线上时,点P的坐标如下:
P1(2.5,0),P2(![]() ,0),P3(9-
,0),P3(9-![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形![]() 的顶点
的顶点![]() 同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边
同时沿正方形的边开始移动,甲按顺时针方向环行,乙按逆时针方向环行,若乙的速度是甲的3倍,那么它们第1次相遇在边![]() 上.
上.

(1)它们第2次相遇在边__________上;
(2)它们第2019次相遇在边__________上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副含30°和45°角的三角尺放置在直线![]() 上.
上.

(1)将图1中的三角尺![]() 绕点
绕点![]() 顺时针方向旋转至如图2所示的位置,
顺时针方向旋转至如图2所示的位置,![]() 在射线
在射线![]() 上,此时
上,此时![]() 旋转的角度为度;
旋转的角度为度;
(2)将图2中的三角尺![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ).
).
①如图3,当![]() 在
在![]() 的内部时,求
的内部时,求![]() 的值;
的值;
②若旋转的速度为每秒15°,经过![]() 秒,当三角尺
秒,当三角尺![]() 与三角尺
与三角尺![]() 的重叠部分以
的重叠部分以![]() 为顶点的角的度数为30°时,求
为顶点的角的度数为30°时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列信息材料
信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来,比如、![]() 、
、![]() 等,而常用的“……”或者“
等,而常用的“……”或者“![]() ”的表示方法都不够百分百准确;
”的表示方法都不够百分百准确;
信息2:![]() 的小数部分是
的小数部分是![]() ,可以看成
,可以看成![]() 得来的:
得来的:
信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如![]() ,是因为
,是因为![]() :
:
根据上述信息,回答下列问题:
(1)若![]() ,则
,则![]() 的小数部分可以表示为_______;
的小数部分可以表示为_______;
(2)![]() 也是夹在两个整数之间的,可以表示为
也是夹在两个整数之间的,可以表示为![]() 则
则![]() _______;
_______;
(3)若![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,请求
,请求![]() 的相反数.
的相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com