
����Ŀ����ͼ����ֱ������ϵxOy�У�����OABC�Ķ���A��C�ֱ���x���y���������ϣ���B�������ǣ�5��2������P��CB����һ���㣨�����C����B�غϣ�������OP��AP������O������OE��AP���ӳ����ڵ�E����CB���ڵ�M���ҡ�AOP=��COM����CP=x��MP=y��
��1����xΪ��ֵʱ��OP��AP��
��2����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��3���ڵ�P���˶������У��Ƿ����x��ʹ��OCM��������ABP�����֮�͵��ڡ�EMP������������ڣ�����x��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������֪��OA=BC=5��AB=OC=2����B=��OCM=90�㣬BC��OA��
��OP��AP��
���OPC+��APB=��APB+��PAB=90�㣬
���OPC=��PAB��
���OPC�ס�PAB��
�� ![]() ����
���� ![]() ��
��
���x1=4��x2=1���������⣬��ȥ����
�൱x=4ʱ��OP��AP
��2��
�⣺��BC��OA��
���CPO=��AOP��
�ߡ�AOP=��COM��
���COM=��CPO��
�ߡ�OCM=��PCO��
���OCM�ס�PCO��
�� ![]() ����
���� ![]() ��
��
�� ![]() ��x��ȡֵ��Χ��2��x��5��
��x��ȡֵ��Χ��2��x��5��
��3��
�⣺�������x�������⣬
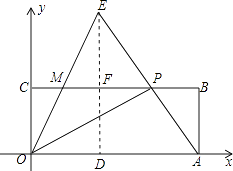
��E��ED��OA�ڵ�D����MP�ڵ�F����DF=AB=2��
�ߡ�OCM���ABP���֮�͵��ڡ�EMP�������
�� ![]() ��
��
��ED=4��EF=2��
��PM��OA��
���EMP�ס�EOA��
�� ![]() ����
���� ![]() ��
��
��� ![]() ��
��
���ɣ�2�� ![]() �ã�
�ã� ![]() ��
��
��� ![]() ������������ȥ����
������������ȥ����
���ڵ�P���˶������У����� ![]() ��ʹ��OCM���ABP���֮�͵��ڡ�EMP�������
��ʹ��OCM���ABP���֮�͵��ڡ�EMP�������
����������1���������������ε��ж�����֤����OPC�ס�PAB���������������ε������г�����ʽ���õ�һԪ���η��̣��ⷽ�̼��ɣ���2��֤����OCM�ס�PCO���������������ε������г�����ʽ������⣻��3����E��ED��OA�ڵ�D����MP�ڵ�F����������õ���EOA�����=����OABC����������ED�ij����������������ε��������PM���ɣ�2���Ľ���ʽ���㼴�ɣ�
�����㾫����������Ŀ����֪�������������������ε�Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ˮ��������������A�е�һ��ˮ�������������ۣ��л������������䷽ʽ����������е���ľ�Ϊ200Ԫ/ʱ��������Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶ� (ǧ��/ʱ) | �˷� (Ԫ/ǧ��) | װж���� (Ԫ) |
�� | 100 | 15 | 2000 |
���� | 80 | 20 | 900 |
(1)���ѡ���������ܷ��ñ�ѡ����ܷ��ö�1100Ԫ����ô��֪��������A��֮���·���Ƕ���ǧ���������з��̽��
(2)��A����ij��֮���·��Ϊsǧ�ף���֪������������·�ϵ����ʱ��ֱ�Ϊ2Сʱ��3.1Сʱ��Ҫ�뽫����ˮ���������н������ۣ���sΪ����ʱ��ѡ��������������������ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�죬С��ȥ���Ѽҽ��飬�����Ѽ�ͣ��һ��ʱ����ؼ��У���ͼ������ҵ�·�� ��ǧ�ף���ʱ�� ���֣���ϵ��ͼ����ͼ����Ϣ������˵����ȷ���� ( )
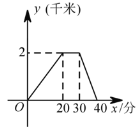
A. С��ȥʱ���ٶȴ��ڻؼҵ��ٶ� B. С��ȥʱ������·���ؼ�ʱ������·
C. С��ȥʱ����ʱ�����ڻؼ�����ʱ�� D. С�������Ѽ�ͣ���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0������A����1��0����B��3��0����C��0����3�����㣬ֱ��l�������ߵĶԳ��ᣮ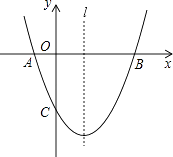
��1���������ߵĺ�����ϵʽ��
��2�����P��ֱ��l�ϵ�һ�����㣬����P����A����B�ľ���֮�����ʱ�����P�����ꣻ
��3����MҲ��ֱ��l�ϵĶ��㣬�ҡ�MACΪ���������Σ���ֱ��д�����з��������ĵ�M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֣�

��1����ѧ����ϣ�С������֪��ABO(��ͼ1)�Ƶ�O��ת180���õ���CDO(��ͼ2)��С�������߶�AB��CD������Ĺ�ϵ������д�����߶�AB��CD�Ĺ�ϵ�� ��
��2������AD����ͼ3�����۲�ͼ�Σ���˵��AB+AD��2AO��
��3������BC����ͼ4�����۲�ͼ�Σ�ֱ��д��ͼ��ȫ�ȵ������Σ�
��д�����Լ��ɣ� ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ж�AB��CD�������У� ������
��1����B+��BCD=180������2����1=��2����3����3=��4����4����B=��5��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD=![]() AB=
AB= ![]() CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�����axym�ǹ���x��y�ĵ���ʽ����ϵ����4��������5����ôa��m��ֵ�ֱ���________��
(2)�����(a��2)xym�ǹ���x��y����ε���ʽ����ôa��mӦ�����������____________��
(3)�������ʽ2x3y4�룭![]() x2zn�Ĵ�����ͬ����ôn��________.
x2zn�Ĵ�����ͬ����ôn��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������֪��ABC�ǵ��������Σ���BAC=90������D��BC���е㣬��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��1���Բ����߶�BG��AE��������ϵ��
��2����ͼ������������DEFG�Ƶ�D����ʱ�뷽����ת����0�㣼����90�������жϣ�1���еĽ����Ƿ���Ȼ������֤����Ľ��ۣ�

(3)��BC=DE=2,�ڣ�2������ת������,���߶�AE�������ֵ����Сֵ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com