
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C.
(1)求证:BE=CE;
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N,若AB=2.(如图2)
①求证:四边形EMBN的面积为定值;
②设BM=x,△EMN面积为S,求S最小值.

【答案】(1)见解析;(2)①见解析;②2.
【解析】
(1)由矩形的性质得出AB=DC,∠A=∠D=90°,由E是AD中点得出AE=DE,由SAS证得△BAE≌△CDE,即可得出结论;
(2)①由(1)可知△EBC是等腰直角三角形,易证△ABE是等腰直角三角形,得出∠EBC=∠ECN=∠EBM=45°,证明∠MEB=∠NEC,由ASA证得△BEM≌△CEN,得出S四边形EMBN=S△EBC,求出BE=CE=![]() ,则S四边形EMBN=S△EBC=
,则S四边形EMBN=S△EBC=![]() BECE=4,即可得出结论;
BECE=4,即可得出结论;
②由①知△BEM≌△CEN,BE=CE=![]() ,则BM=CN=x,BC=
,则BM=CN=x,BC=![]() BE=4,BN=4﹣x,S=S四边形EMBN﹣S△BMN=4﹣
BE=4,BN=4﹣x,S=S四边形EMBN﹣S△BMN=4﹣![]() BMBN=
BMBN=![]() (x﹣2)2+2,由
(x﹣2)2+2,由![]() >0,则当x=2时,S有最小值为2.
>0,则当x=2时,S有最小值为2.
(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵E是AD中点,
∴AE=DE,在△BAE和△CDE中,
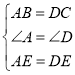 ,
,
∴△BAE≌△CDE(SAS),
∴BE=CE;
(2)①证明:由(1)可知,△EBC是等腰直角三角形,
∴∠EBC=45°,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
∴∠ABE=90°﹣45°=45°,
∴△ABE是等腰直角三角形,
∴∠EBC=∠ECN=∠EBM=45°,
∵∠MEB+∠BEN=90°,∠NEC+∠BEN=90°,
∴∠MEB=∠NEC,
在△BEM和△CEN中,
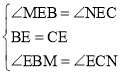 ,
,
∴△BEM≌△CEN(ASA),
∴S四边形EMBN=S△EBC,
∵AB=2,
∴BE=CE=![]() ,
,
∴S四边形EMBN=S△EBC=![]() BECE=
BECE=![]() ×2
×2![]() ×2
×2![]() =4,
=4,
∴四边形EMBN的面积为定值;
②解:由①知,△BEM≌△CEN,BE=CE=![]() ,
,
∴BM=CN=x,BC=![]() BE=
BE=![]() ×2
×2![]() =4,
=4,
∴BN=4﹣x,
∴S=S四边形EMBN﹣S△BMN=4﹣![]() BMBN=4﹣
BMBN=4﹣![]() x(4﹣x)=
x(4﹣x)=![]() x2﹣2x+4=
x2﹣2x+4=![]() (x﹣2)2+2,
(x﹣2)2+2,
∵![]() >0,
>0,
∴当x=2时,S有最小值为2.


科目:初中数学 来源: 题型:
【题目】端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程y(单位:米)与时间t(单位:分)之间的函数关系式如图所示,根据图中提供的信息,有下列说法:①甲队比乙队提前0.5分到达终点②当划行1分钟时,甲队比乙队落后50米③当划行![]() 分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
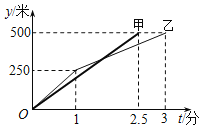
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
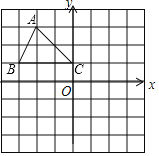
【题目】如图,在平面直角坐标系中,△ABC三个顶点都在格点上,点A,B,C的坐标分别为A(﹣2,3),B(﹣3,1),C(0,1)请解答下列问题:
(1)△ABC与△A1B1C1关于原点O成中心对称,画出△A1B1C1并直接写出点A的对应点A1的坐标;
(2)画出△ABC绕点C顺时针旋转90°后得到的△A2B2C,并求出线段AC旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
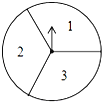
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.小明和小华利用这个转盘做游戏,若采用下列游戏规则:小明和小华各转一次,指针各指向一个数字,如果两数字之和是奇数是小明胜,否则小华胜。
(1)请用列表或画树状图的方法列出所有可能的情况;
(2)你认为这个游戏对双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
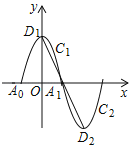
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和3,点D在CE上,且∠A=120°,B,C,G三点在同一直线上,则BD与CF的位置关系是_____;△BDF的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
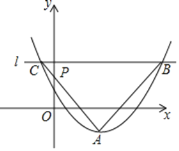
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角为直角的四边形叫做“对直角四边形”.如图1,四边形ABCD中,∠A=∠C=90°,则四边形ABCD是“对直角四边形”.

(1)“对角线相等的对直角四边形是矩形”是______命题;(填“真”或“假”)
(2)如图2,在对直角四边形ABCD中,∠DAB<90°,AD+CD=AB+BC.试说明△ADC的面积与△ABC的面积相等;
(3)如图3,在△ABC中,∠C=90°,AC=6,BC=8,过AB的中点D作射线DP∥AC,交BC于点O,∠BDP与∠ADP的角平分线分别交BC,AC于点E、F.
①图中是“对直角四边形”的是______;
②当OP的长是______时,四边形DEPF为对直角四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com