
【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩.根据统计图中的信息可得,下列结论正确的是( )

A. 甲队员成绩的平均数比乙队员的大
B. 甲队员成绩的方差比乙队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 乙队员成绩的方差比甲队员的大
【答案】B
【解析】
根据平均数的公式:平均数=所有数之和再除以数的个数;方差就是各变量值与其均值离差平方的平均数,根据方差公式计算即可;中位数就是最中间的数或最中间两个数的平均数.
(1)甲队员10次射击的成绩分别为6,7、7,7,8,8,9,9,9,10;
甲10次射击成绩的平均数=(6+3×7+2×8+3×9+10)÷10=8,
方差=![]() [(6-8)2+3×(7-8)2+2×(8-8)3+3×(9-8)2+(10-8)2]=1.4;
[(6-8)2+3×(7-8)2+2×(8-8)3+3×(9-8)2+(10-8)2]=1.4;
中位数:8.
(2)乙队员9次射击的成绩分别为6,7,7,8,8,8,9,9,10;
乙9次射击成绩的平均数=(6+2×7+3×8+2×9+10)÷9=8,
方差=![]() [(6-8)2+2×(7-8)2+3×(8-8)3+2×(9-8)2+(10-8)2]≈1.3;
[(6-8)2+2×(7-8)2+3×(8-8)3+2×(9-8)2+(10-8)2]≈1.3;
中位数:8.
两者平均数和中位数相等,甲的方差比乙大.
故选:B


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
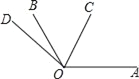
【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y= ![]() 图象恰好过点D,则k的值为( )
图象恰好过点D,则k的值为( ) 
A.6
B.﹣6
C.9
D.﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
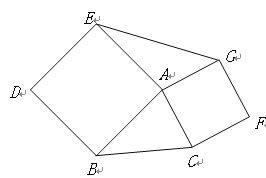
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?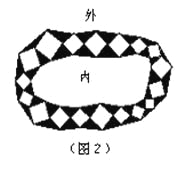
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
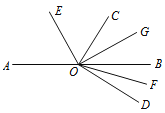
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
查看答案和解析>>
科目:初中数学 来源: 题型:
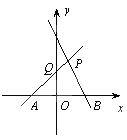
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
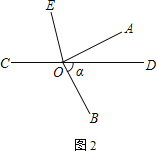
【题目】已知O是直线上的一点,∠AOB是直角,OE平分∠AOC
(1) 在图①中,若∠BOD=28°,求∠AOE的度数
(2) 将图①中的∠AOB绕顶点O顺时针旋转至图②的位置.若∠BOD=α,试用含α的式子表示∠AOE,并说明理由
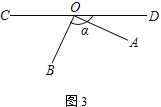
(3) 继续旋转AOB至图③的位置,若∠BOD=α,其他条件不变,试将图形补充完整,求∠AOE的度数.(用含α的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com