
【题目】我们知道,如果两个三角形全等,则它们面积相等,而两个不全等的三角形,在某些情况下,可通过证明等底等高来说明它们的面积相等.已知△ABC与△DEC是等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE. 
(1)如图1,当∠BCE=90°时,求证:S△ACD=S△BCE;
(2)如图2,当0°<∠BCE<90°时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
(3)如图3,在(2)的基础上,作CF⊥BE,延长FC交AD于点G,求证:点G为AD中点.
【答案】
(1)证明:∵△ABC与△DEC是等腰直角三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE
∵∠BCE=90°,
∴∠ACE=∠BCE,
在△ACD与△BCE中,
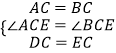 ,
,
∴△ACD≌△BCE(SAS),
∴S△ACE=S△BCE
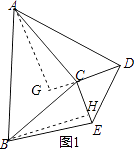
(2)证明:作AG垂直DC的延长线于点G,作BH⊥CE,垂足为H,
∵∠ACB=∠GCE=90°,
∴∠ACG=∠BCH,
在△ACG与△BCF中,
 ,
,
∴△ACG≌△BCH(AAS)
∴AG=BH
∵CD=CE
∴ ![]() CDAG=
CDAG= ![]() CEBH,
CEBH,
即S△ACE=S△BCE
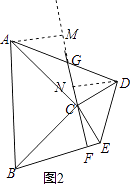
(3)证明:作AM垂直CG的延长线于点M,作DN⊥CG,垂足为N,
∴∠ACB=90,∠BFC=90°,
∴∠ACM+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACM=∠CBF,
在△ACM与△BCF中,
 ,
,
∴△ACM≌△CBF(AAS),
∴AM=CF,
同理可证△DCN≌△CEF,
∴DN=CF,
∴AM=DN,
又∵∠AMG=∠DNG,
∴∠AGM=∠DGN,
在△AMG与△DNG中,
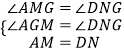 ,
,
∴△AMG≌△DNG(AAS),
∴AG=DG,
即G为AD中点,
【解析】(1)根据△ABC与△DEC是等腰直角三角形,得到AC=BC,DC=EC,∠ACB=∠DCE由∠BCE=90°,证得∠ACE=∠BCE,推出△ACD≌△BCE,从而证得结论S△ACE=S△BCE;(2)作AG垂直DC的延长线于点G,作BH⊥CE,垂足为H,由于∠ACB=∠GCE=90°,得到∠ACG=∠BCH,推出△ACG≌△BCH,得出AG=BH,由于CD=CE,于是得到结果即S△ACE=S△BCE;(3)作AM垂直CG的延长线于点M,作DN⊥CG,垂足为N,证得△ACM≌△CBF,得到AM=CF,同理可证△DCN≌△CEF,得到DN=CF,AM=DN,推出△AMG≌△DNG,得到AG=DG,即G为AD中点.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
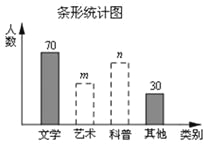
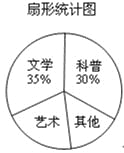
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() 、
、![]() 对应的数分别为
对应的数分别为![]() ,
, ![]() ,点
,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
(![]() )若点
)若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,直接写出点
的距离相等,直接写出点![]() 对应的数.
对应的数.
(![]() )数轴上是否存在点
)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() 、点
、点![]() 的距离之和为
的距离之和为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )现在点
)现在点![]() 、点
、点![]() 分别以
分别以![]() 个单位长度/秒和
个单位长度/秒和![]() 个单位长度/秒的速度同时向右运动,点
个单位长度/秒的速度同时向右运动,点![]() 以
以![]() 个单位长度/秒的速度同时从
个单位长度/秒的速度同时从![]() 点向左运动.当点
点向左运动.当点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度时,求点
个单位长度时,求点![]() 所对应的数是多少?
所对应的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( ) 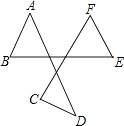
A.180°
B.360°
C.540°
D.720°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.

如果图1中的圆圈共有12层,
(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__;
(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.

(1)求∠ABC的度数;
(2)A船以每小时40海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com