
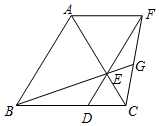
 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、CF,联结BE并延长交CF于点G
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、CF,联结BE并延长交CF于点G分析 ①由△ABC是等边三角形,得出∠BAC=∠ACB=60°,即可证得△DEC是等边三角形,得出∠DEC=∠AEF=60°,证得△AEF是等边三角形,再由SAS证得△ABE≌△ACF;
②由△ABC与△DEC都是等边三角形,得出∠ABC=∠FDC=60°,证得AB∥DF,再由△ABC与△AEF都是等边三角形,得出∠EAF=∠ACB=60°,证得AB∥AF,
得出四边形ABDF是平行四边形即可;
③由△ABE≌△ACF,得出BE=CF,S△ABE=S△ACF,再由SSS证得△BCE≌△DCF,得出S△BCE=S△DCF,即可得出结论;
④证明△BDE∽△FGE,得$\frac{BD}{FG}$=$\frac{DE}{EG}$,由此即可得出结论.
解答 解:①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴ED=EC=DC,∠DEC=∠AEF=60°,
∵EF=AE,
∴△AEF是等边三角形,
∴AF=AE,∠EAF=60°,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAF}\\{AE=AF}\end{array}\right.$,
∴△ABE≌△ACF(SAS),
故①正确;
②∵△ABC与△DEC都是等边三角形,
∴∠ABC=∠FDC=60°,
∴AB∥DF,
∵△ABC与△AEF都是等边三角形,
∴∠EAF=∠ACB=60°,
∴AB∥AF,
∴四边形ABDF是平行四边形,
∴DF=AB=BC,
故②正确;
③∵△ABE≌△ACF,
∴BE=CF,S△ABE=S△ACF,
在△BCE和△DCF中,
$\left\{\begin{array}{l}{BC=DF}\\{CE=CD}\\{BE=CF}\end{array}\right.$,
∴△BCE≌△DCF(SSS),
∴S△BCE=S△DCF,
∴S△ABC=S△ABE+S△BCE=S△ACF+S△DCF,
故③正确;
④正确.∵△BCE≌△FDC,
∴∠DBE=∠EFG,
∵∠BED=∠FEG,
∴△BDE∽△FGE,
∴$\frac{BD}{FG}$=$\frac{DE}{EG}$,
∴$\frac{FG}{EG}$=$\frac{BD}{DE}$,
∵BD=2DC,DC=DE,
∴$\frac{FG}{EG}$=2,
∴FG=2EG,
故④错误;
综上所述,正确的结论是:①②③.
点评 本题考查全等三角形的判定和性质、等边三角形的判定与性质、相似三角形的判定和性质、平行线的判定、平行四边形的判定和性质等知识,熟练掌握与灵活应用这些知识是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为40°或100°或70°.
如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为40°或100°或70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com