
分析 原式逆用乘法分配律计算即可;
原式变形后,利用乘法分配律计算即可得到结果;
原式利用乘法交换律与结合律计算即可;
原式先计算除法运算,再计算加法运算即可.
解答 解:原式=4×(6.5+3.5)-17=40-17=23;
原式=(86+1)×$\frac{3}{86}$=3+$\frac{3}{86}$=3$\frac{3}{86}$;
原式=(25×$\frac{2}{5}$)×($\frac{1}{3}$×$\frac{3}{10}$)=10×$\frac{1}{10}$=1;
原式=4.25+14.5=18.75.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
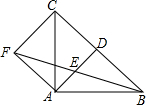 如图,在△ABC中,D是边BC的中点,连接AD,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
如图,在△ABC中,D是边BC的中点,连接AD,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.
如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
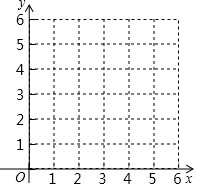 四边形ABCD各顶点的坐标分别为A(0,1),B(5,1),C(6,3),D(2,5).
四边形ABCD各顶点的坐标分别为A(0,1),B(5,1),C(6,3),D(2,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com