Question

18．已知点M（6-2a，a+1）关于y轴的对称点在第一象限，则a的取值范围在数轴上表示正确的是（　　）

• A．
• B．
• C．
• D．

Answer 1

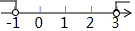分析 根据关于y轴对称的点确定出点M在第二象限，然后根据第二象限内点的横坐标是负数，纵坐标是正数列不等式组求出a的取值范围，然后选择即可．

解答 解：∵点M（6-2a，a+1）关于y轴的对称点在第一象限，
∴点M在第二象限，
∴$\left\{\begin{array}{l}{6-2a＜0①}\\{a+1＞0②}\end{array}\right.$，
解不等式①得，a＞3，
解不等式②得，a＞-1，
在数轴上表示如下，
故选B．

点评 本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；
（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．