若两个相似多边形的对应边的比是5:4.则这两个多边形的面积比是．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

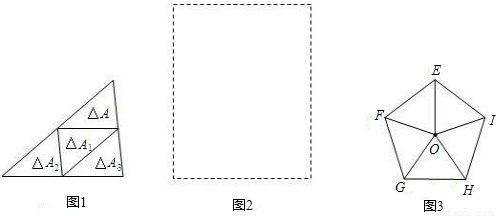
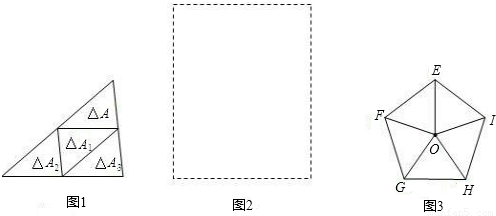
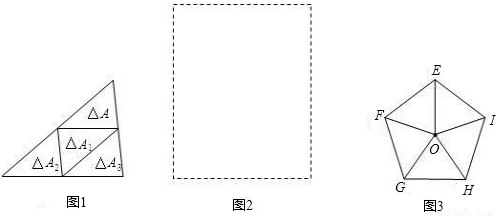
27、我们约定，若一个三角形（记为△A₁）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A₁，又由△A₁复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，它用到

1

次平移，

2

次旋转．小明发现△B∽△A，其相似比为

2：1

．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有

121

个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是

正三边形、正六边形

；
（3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
（4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

查看答案和解析>>

科目：初中数学 来源：第25章《图形的变换》中考题集（15）：25.2 旋转变换（解析版） 题型：解答题

我们约定，若一个三角形（记为△A₁）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A₁，又由△A₁复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，它用到______次平移，______次旋转．小明发现△B∽△A，其相似比为______．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是______；
（3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
（4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

查看答案和解析>>

科目：初中数学 来源：第29章《相似形》中考题集（19）：29.5 相似三角形的性质（解析版） 题型：解答题

我们约定，若一个三角形（记为△A₁）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A₁，又由△A₁复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，它用到______次平移，______次旋转．小明发现△B∽△A，其相似比为______．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是______；
（3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
（4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

查看答案和解析>>

科目：初中数学 来源：第3章《图形的相似》中考题集（18）：3.3 相似三角形的性质和判定（解析版） 题型：解答题

我们约定，若一个三角形（记为△A₁）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A₁，又由△A₁复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，它用到______次平移，______次旋转．小明发现△B∽△A，其相似比为______．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是______；
（3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
（4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

查看答案和解析>>

科目：初中数学 来源：第4章《相似三角形》中考题集（19）：4.3 两个三角形相似的判定（解析版） 题型：解答题

我们约定，若一个三角形（记为△A₁）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A₁，又由△A₁复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，它用到______次平移，______次旋转．小明发现△B∽△A，其相似比为______．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是______；
（3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
（4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

查看答案和解析>>

练习册

高中

初中

小学