
已知抛物线y = x2-2x + m-1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.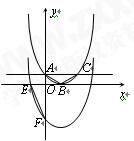
(1)∵抛物线y = x2-2x + m-1与x轴只有一个交点,∴△=(-2)2-4×1×(m-1)= 0,解得 m = 2.
(2)由(1)知抛物线的解析式为 y = x2-2x + 1,易得顶点B( 1,0),当 x = 0时,y = 1,得A(0,1).
1,0),当 x = 0时,y = 1,得A(0,1).
由 1 = x2-2x + 1 解得 x = 0(舍),或 x = 2,所以C(2,1).
过C作x轴的垂线,垂足为D,则CD = 1,BD = xD-xB = 1.
∴在Rt△CDB中,∠CBD = 45°,BC =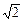 .
.
同理,在Rt△AOB中,AO =" OB" = 1,于是∠ABO  = 45°,AB =
= 45°,AB =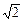 .
.
∴∠ABC = 180°-∠CBD-∠ABO = 90°,AB = BC,因此△ABC是等腰直角三角形.
(3)由题知,抛物线C′ 的解析式为y = x2-2x -3,当 x = 0时,y =-3;当y = 0时,x =-1,或x = 3,
∴ E(-1, 0),F(0,-3),即 OE = 1,OF = 3.
0),F(0,-3),即 OE = 1,OF = 3.
①若以E点为直角顶点,设此时满足条件的点为P1(x1,y1),作P1M⊥x轴于M.
∵∠P1EM +∠OEF =∠EFO +∠OEF = 90°,
∴∠P1EM =∠EFO,得Rt△EFO∽Rt△P1EM,于是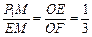 ,即EM =" 3" P1M.
,即EM =" 3" P1M.
∵ EM = x1 + 1,P1M = y1,∴ x1 + 1 =" 3" y1. (*)
由于P1(x1,y1)在抛物线C′ 上,有3(x12-2x1-3)= x1 + 1,
整理得 3x12-7x1-10 = 0,解得 x1 =-1(舍),或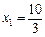 .
.
把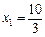 代人(*)中可解得
代人(*)中可解得
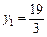 .∴P1(
.∴P1( ,
,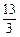 ).
).
② 若以F点为直角顶点,设此时满足条件的点为P2(x2,y2),作P2N⊥与y轴于N.
若以F点为直角顶点,设此时满足条件的点为P2(x2,y2),作P2N⊥与y轴于N.
同①,易知Rt△EFO∽Rt△FP2N,得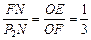 ,即P2N =" 3" FN.
,即P2N =" 3" FN.
∵ P2N = x2,FN =" 3" + y2,∴ x2 = 3(3 + y2). (**)
由于P2(x2,y2)在 抛物线C′ 上,有 x2 = 3(3 + x22-2x2-3),
抛物线C′ 上,有 x2 = 3(3 + x22-2x2-3),
整理得 3x22-7x2 = 0,解得 x2 = 0(舍),或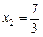 .
.
把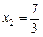 代人(**)中可解得
代人(**)中可解得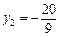 .∴P2(
.∴P2(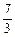 ,
, ).
).
综上所述,满足条件的P点的坐标为( ,
,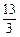 )或(
)或(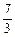 ,
, ).
).
解析


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为| 15 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-| 1 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com