
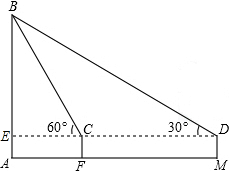
 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高.
如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高. 分析 求出∠CBD=∠BDE,得到△BCD是等腰三角形,从而求出BC的长,然后在△BEC中,求出BE的长,然后求出AB 的长.
解答 解:∵∠BDE=30°,∠BCE=60°,
∴∠CBD=60°-∠BDE=30°=∠BDE,
∴BC=CD=10米,
在Rt△BCE中,sin∠BCD=$\frac{BE}{BC}$,
即BE=BC•sin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$米,
AB=BE+AE=(5$\sqrt{3}$+1)米.
答:旗杆AB的高度是(5$\sqrt{3}$+1)米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,会解直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com