
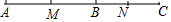 已知M是线段AB的中点,N是线段BC的中点.
已知M是线段AB的中点,N是线段BC的中点.分析 本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据正确画出的图形解题.
解答 解:(1)分两种情况: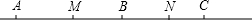 第一种情况:B在AC内,
第一种情况:B在AC内,
则MN=$\frac{1}{2}$AB+$\frac{1}{2}$BC=$\frac{1}{2}$(AB+BC)=8厘米;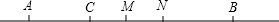 第二种情况:B在AC外,则MN=$\frac{1}{2}$AB-$\frac{1}{2}$BC=$\frac{1}{2}$(AB-BC)=2厘米;
第二种情况:B在AC外,则MN=$\frac{1}{2}$AB-$\frac{1}{2}$BC=$\frac{1}{2}$(AB-BC)=2厘米;
故答案为:8厘米或2厘米.
(2)同(1)得:MN=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$(a+b),或MN=$\frac{1}{2}$(AB-BC)=$\frac{1}{2}$(a-b)(a>b),或MN=$\frac{1}{2}$(BC-AB)=$\frac{1}{2}$(b-a)(b>a),
故答案为:$\frac{1}{2}$(a+b)或$\frac{1}{2}$|a-b|;
(3)由(2)得:MN=$\frac{1}{2}$m.
点评 本题考查了两点间的距离、线段的中点的定义;注意分类讨论,避免漏解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 个 | B. | 3 个 | C. | 4 个 | D. | 5 个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
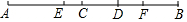 如图,C、D是线段AB上的点,E为AD中点,F为BC中点.
如图,C、D是线段AB上的点,E为AD中点,F为BC中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1-{a}^{2}}{-a}$=$\frac{{a}^{2}-1}{a}$ | B. | $\frac{-1-{a}^{2}}{-a}$=$\frac{1-{a}^{2}}{a}$ | ||
| C. | $\frac{-ab}{a-b}$=$\frac{ab}{b-a}$ | D. | $\frac{(a-b)^{2}}{{a}^{2}-{b}^{2}}$=$\frac{a-b}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com