
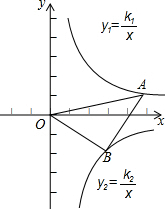
 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
| k1 |
| m |
m2+
|
| k1 |
| 2 |
|
(
|
|
(
|
| ||
| 4 |
| k1 |
| m |
| k1 |
| 2 |
| ||
| m2 |
| 5 |
| 5 |
| 5 |
| 5 |


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
| 1 |
| x-3 |
| x |
| 3-x |
| 2 |
| x+1 |
| 3 |
| 1-x |
| 5 |
| 1-x2 |
| x-3 |
| x-2 |
| 3 |
| 2-x |
| 2x |
| x+1 |
| x |
| 3x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
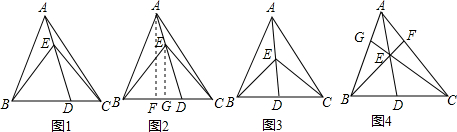
| S四边形ABEC |
| S△ABC |
| EG |
| AF |
| S△BCE |
| S△ABC |
| S四边形ABEC |
| S△ABC |
| AE |
| AD |
| BE |
| BF |
| CE |
| CG |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知AB∥CE,∠A=∠E,求证:∠CGD=∠FHB.
如图所示,已知AB∥CE,∠A=∠E,求证:∠CGD=∠FHB.查看答案和解析>>
科目:初中数学 来源: 题型:
 某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为20米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).
某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为20米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com