
科目:初中数学 来源: 题型:
若记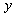 =
=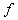 (
(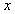 )=
)= ,其中
,其中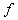 (1)表示当
(1)表示当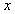 =1时
=1时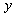 的值,即
的值,即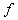 (1)=
(1)=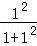 =
= ;
; 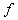 (
( )表示当
)表示当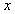 =
= 时
时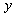 的值,即
的值,即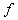 (
( )=
)=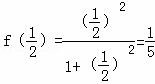 ;…;则
;…;则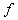 (1)+
(1)+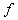 (2)+
(2)+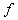 (
( )+
)+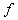 (3)+
(3)+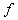 (
(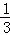 )+…+
)+…+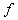 (2011)+
(2011)+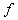 (
( )= ___________.
)= ___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差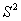 :
:
| 甲 | 乙 | 丙 | 丁 | |
|
| 175 | 173 | 175 | 174 |
| 方差 | 3.5 | 3.5 | 12.5 | 15 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线 的顶点为点C.
的顶点为点C.
(1)求证:不论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)若抛物线的对称轴为直线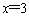 ,求m的值和C点坐标;
,求m的值和C点坐标;
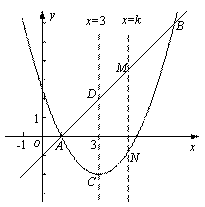
(3)如图,直线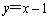 与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线
与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线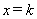 交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.
交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
完成下面的证明.
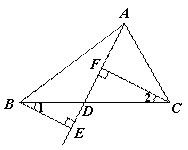
已知:如图, D是BC上任意一点,BE⊥AD,交AD的
延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
证明:∵BE⊥AD ,
∴∠BED= °( ).
∵CF⊥AD,
∴∠CFD= °.
∴∠BED=∠CFD.
∴BE∥CF( ).
∴∠1=∠2( ).
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
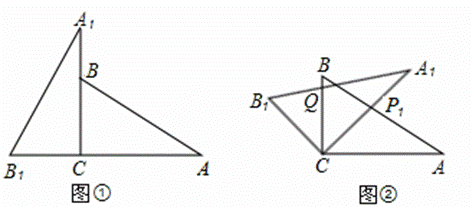
将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com