
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
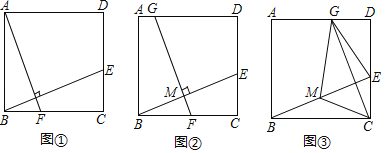
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
【答案】(1)证明见解析;(2)2,9.
【解析】感知:利用同角的余角相等判断出∠BAF=∠CBE,即可得出结论;
探究:(1)判断出PG=BC,同感知的方法判断出△PGF≌CBE,即可得出结论;
(2)利用直角三角形的斜边的中线是斜边的一半,
应用:借助感知得出结论和直角三角形斜边的中线是斜边的一半即可得出结论.
感知:∵四边形ABCD是正方形,
∴AB=BC,∠BCE=∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠BAF=∠CBE,
在△ABF和△BCE中,
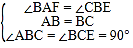 ,
,
∴△ABF≌△BCE(ASA);
探究:(1)如图②,
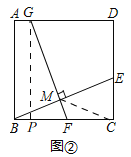
过点G作GP⊥BC于P,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴四边形ABPG是矩形,
∴PG=AB,∴PG=BC,
同感知的方法得,∠PGF=∠CBE,
在△PGF和△CBE中,
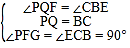 ,
,
∴△PGF≌△CBE(ASA),
∴BE=FG;
(2)由(1)知,FG=BE,
连接CM,
∵∠BCE=90°,点M是BE的中点,
∴BE=2CM=2,
∴FG=2,
故答案为:2.
应用:同探究(2)得,BE=2ME=2CM=6,
∴ME=3,
同探究(1)得,CG=BE=6,
∵BE⊥CG,
∴S四边形CEGM=![]() CG×ME=
CG×ME=![]() ×6×3=9,
×6×3=9,
故答案为:9.


科目:初中数学 来源: 题型:
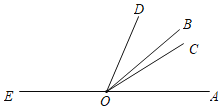
【题目】如图,点O是直线AE上的一点,OC是∠AOD的平分线,∠BOD=![]() ∠AOD.
∠AOD.
(1)若∠BOD=20°,求∠BOC的度数;
(2)若∠BOC=n°,用含有n的代数式表示∠EOD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
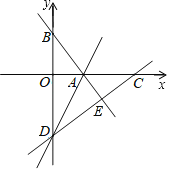
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收贵的价目表如下(注:水费按月份结算,![]() 表示立方米)
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
![]() 某户居民1月份和2月份的用水量分别为
某户居民1月份和2月份的用水量分别为![]() 和
和![]() ,则应收水费分别是 元和 元
,则应收水费分别是 元和 元
![]() 若该户居民
若该户居民![]() 月份用水量
月份用水量![]() (其中
(其中![]() ),则应收水费多少元? (用含
),则应收水费多少元? (用含![]() 的式子表示,并化简)
的式子表示,并化简)
![]() 若该户居民
若该户居民![]() 两个月共用水
两个月共用水 ![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 两个月共交水费多少元? (用含
两个月共交水费多少元? (用含 ![]() 的式子表示,并化简)
的式子表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
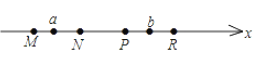
【题目】如图,![]() 分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数
分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数![]() 对应的点在
对应的点在![]() 与
与![]() 之间,数
之间,数![]() 对应的点在
对应的点在![]() 与
与![]() 之间.若
之间.若![]() ,则原点是( )
,则原点是( )
A.![]() 或
或![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
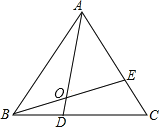
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
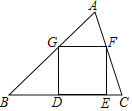
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com