
 如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.
如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.分析 (1)BG=CH,连接BD,利用等腰直角三角形的性质可以证明△BDH≌△CDG,然后利用全等三角形的性质可以得到BH=CG;
(2)根据(1)的结论容易得到S四边形GCHD=S△BDC,而S△BDC可以根据已知条件直接求出,所以四边形GCHD的面积就可以求出了.
解答 解:连接CD.
(1)∵△ABC为等腰直角三角形,且D是AB的中点,
∴∠B=∠ACD=45°,BD=CD,∠BDH+∠CDH=90°,
又因为∠EDC+∠CDH=90°,
∴∠BDH=∠CDG.
在△BDH和△CDG中,$\left\{\begin{array}{l}{∠B=∠GCD}\\{DB=DC}\\{∠BDH=∠CDG}\end{array}\right.$,
∴△BDH≌△CDG.
∴BH=CG.
(2)在旋转过程中四边形GCHD的面积不变,
∵△BDH≌△CDG,
∴四边形GCHD的面积=△CDB的面积.
∵D是AB的中点,
∴△CBD的面积=$\frac{1}{2}$S△ABC=$\frac{1}{2}×4×4×\frac{1}{2}$=4cm2.
∴S四边形GCHD=4cm2.
点评 此题考查了全等三角形的性质与判定,等腰直角三角形的性质,三角形的面积公式,还有图形变换,证得△BDH≌△CDG是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
 已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.
已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=BC,点D在线段BC上,连接AD,过点D作AD的垂线,过点B作AB的垂线,两条垂线相交于点E,若BD=2CD,且AC=3,过点B作BF⊥BC交AE于点F,连接DF,求DF的长.
如图,在△ABC中,∠C=90°,AC=BC,点D在线段BC上,连接AD,过点D作AD的垂线,过点B作AB的垂线,两条垂线相交于点E,若BD=2CD,且AC=3,过点B作BF⊥BC交AE于点F,连接DF,求DF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{2}{x}^{2}$+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=$\frac{1}{2}{x}^{2}$+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
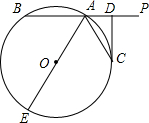 如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.
如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
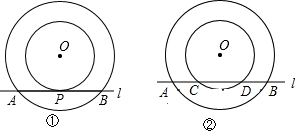 我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.
我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com