
【题目】计算:(1)∣—6∣+(![]() —3.14)0—(
—3.14)0—(![]() )-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
)-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
(3)![]() (4)(a-2b)(a+b)-3a(a+b)
(4)(a-2b)(a+b)-3a(a+b)
【答案】(1)-10;(2)3a5;(3)-6a3b2+10a3b3-2a2;(4)-2a2+2b2
【解析】
(1)原式利用求绝对值,零指数幂、负指数幂法则,乘方运算法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,先算乘方,再算乘除,最后算加减,合并即可得到结果
(3)原式利用单项式乘多项式法则计算即可得到结果
(4)原式利用单项式乘多项式、多项式乘多项式法则计算即可得到结果.
(1)∣—6∣+(![]() -3.14)0—(
-3.14)0—(![]() )-2+(-2)3 =6+1-9 -8 =-10
)-2+(-2)3 =6+1-9 -8 =-10
(2)![]() =-a5+
=-a5+![]() =-a5+4a5=3a5
=-a5+4a5=3a5
(3) ![]() =-6a3b2+10a3b3-2a2
=-6a3b2+10a3b3-2a2
(4) (a+2b)(a+b)-3a(a+b)=a2+ab+2ab+2b2-3a2-3ab=-2a2+2b2


科目:初中数学 来源: 题型:
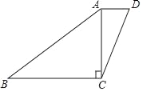
【题目】如图,一张四边形纸片ABCD,AB=20,BC=16,CD=13,AD=5,对角线AC⊥BC.
(1)求AC的长;
(2)求四边形纸片ABCD的面积;
(3)若将四边形纸片ABCD沿AC剪开,拼成一个与四边形纸片ABCD面积相等的三角形,直接写出拼得的三角形各边高的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为 ( )
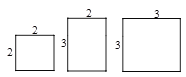
A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
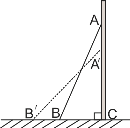
【题目】如图,一架2.5米长的梯子AB 斜靠在一座建筑物上,梯子底部与建筑物距离BC 为0.7米.
(1)求梯子上端A到建筑物的底端C的距离(即AC的长);
(2)如果梯子的顶端A沿建筑物的墙下滑0.4米(即AA′=0.4米),则梯脚B将外移(即BB′的长)多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣8)+3+10+(﹣2)
(2)(﹣2)×(﹣6)÷(﹣![]() )
)
(3)(﹣1)100×2+(﹣2)3÷4
(4)2(a﹣3b)+3(2b﹣3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,原价560元.随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:

(1)根据图像完成下表
降价/元 | 5 | 10 | 15 | |
日销售量/件 | 780 | 840 | 870 |
(2)售价为560元时,日销售量为多少件.
(3)如果该商场要求日销售量为1110件,该商品应降价多少元.
(4)设该商品的售价为![]() 元,日销售量为
元,日销售量为![]() 件,求
件,求![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
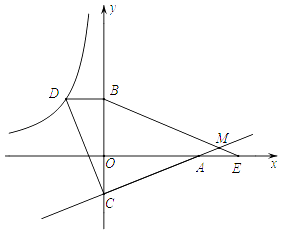
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com