Question

8．已知如图，二次函数图象经过点A（-6，0），B（0，6），对称轴为直线x=-2，顶点为点C，点B关于直线x=-2的对称点为点D．
（1）求二次函数的解析式以及点C和点D的坐标；
（2）联结AB、BC、CD、DA，点E在线段AB上，联结DE，若DE平分四边形ABCD的面积，求线段AE的长；
（3）在二次函数的图象上是否存在点P，能够使∠PCA=∠BAC？如果存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）由二次函数对称轴为直线x=2，根据A坐标确定出二次函数与x轴的另一个交点坐标，设出二次函数解析式为y=a（x+6）（x-2），把C坐标代入求出a的值，确定出二次函数解析式，进而确定出C与D坐标即可；
（2）连接AB、BC、CD、DA，点E在线段AB上，连接DE，如图1所示，利用勾股定理求出AB，BC，CD与BD的长，根据直线CD与直线AB斜率相等，得到DC与AB平行，继而得到四边形ABCD为直角梯形，若DE平分四边形ABCD的面积，可得直角梯形面积等于三角形ADE面积的2倍，求出AE的长即可；
（3）在二次函数的图象上存在点P，能够使∠PCA=∠BAC，如图2所示，直线CP与AB交于点G，可得GA=GC，根据直线AB解析式设出G坐标（x，x+6），利用两点间的距离公式求出x的值，确定出G坐标，利用待定系数法求出直线CG解析式，与二次函数解析式联立求出P坐标；由（2）得到四边形ABCD为直角梯形，即DC与AB平行，利用两直线平行内错角相等，得到P与D重合时，满足题意，确定出此时P的坐标即可．

解答 解：（1）∵二次函数经过A（-6，0），B（0，6），对称轴为直线x=2，
∴二次函数图象经过（2，0），
设二次函数解析式为y=a（x+6）（x-2），
把B（0，6）代入得：6=-12a，即a=-$\frac{1}{2}$，
∴二次函数解析式为y=-$\frac{1}{2}$（x+6）（x-2）=-$\frac{1}{2}$x²-2x+6=-$\frac{1}{2}$（x+2）²+8，
则C（-2，8），D（-4，6）；
（2）如图1所示，由题意得：AB=6$\sqrt{2}$，BC=CD=2$\sqrt{2}$，BD=4，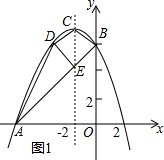

∵BD²=CD²+BC²，
∴∠DCB=90°，
∵直线AB的解析式为y=x+6，直线DC解析式为y=x+10，
∴DC∥AB，
∴四边形ABCD为直角梯形，
若S_梯形ABCD=2S_△ADE，即$\frac{1}{2}$×2$\sqrt{2}$×（2$\sqrt{2}$+6$\sqrt{2}$）=2×$\frac{1}{2}$×2$\sqrt{2}$×AE，
解得：AE=4$\sqrt{2}$；
（3）如图2，在二次函数的图象上存在点P，使∠PCA=∠BAC，直线CP与AB交于点G，可得GA=GC，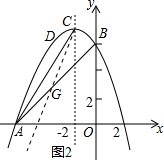

∵A（-6，0），C（-2，8），直线AB解析式为y=x+6，设G（x，x+6），
∴$\sqrt{（x+6）^{2}+（x+6）^{2}}$=$\sqrt{（x+2）^{2}+（x-2）^{2}}$，
两边平方得：2x²+24x+72=2x²+8，
移项合并得：24x=-64，
解得：x=-$\frac{8}{3}$，经检验是原方程的根且符合题意，
∴G（-$\frac{8}{3}$，$\frac{10}{3}$），
设直线CG解析式为y=kx+b，
把C与G坐标代入得：$\left\{\begin{array}{l}{-\frac{8}{3}k+b=\frac{10}{3}}\\{-2k+b=8}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=7}\\{b=22}\end{array}\right.$，
∴直线CG解析式为y=7x+22，
联立得：$\left\{\begin{array}{l}{y=7x+22}\\{y=-\frac{1}{2}{x}^{2}-2x+6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-16}\\{y=-90}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=8}\end{array}\right.$（经检验不合题意，舍去），
∴P坐标为（-16，-90）；
由（2）得到四边形ABCD为直角梯形，AB∥CD，
∴∠DCA=∠BAC，
此时P与D重合，即P（-4，6），
综上，满足题意P的坐标为（-16，-90）或（-4，6）．

点评 此题属于二次函数综合题，涉及的知识有：待定系数法确定二次函数解析式，待定系数法确定一次函数解析式，直角梯形的判定，直线与二次函数的交点，坐标与图形性质，熟练掌握待定系数法是解本题的关键．