
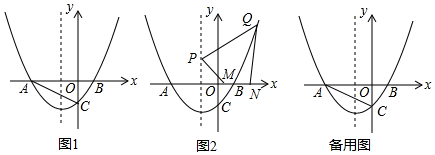
分析 (1)如图1,把T的坐标代入解析式,求出a的值,写出解析式;
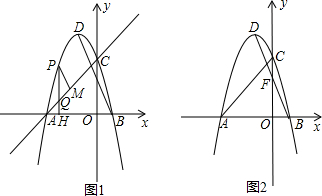
(2)根据点D在第二象限,∠DAB为钝角,所以当A、B、D三点为顶点的三角形与△ABC相似时,只能∠DAB与∠ACB对应,所以分以下两种情况讨论:①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,分别列比例式,得方程求解;
(3)先求出Q的坐标为(6,10),通过轴对称作出使四边形PQNM的周长最小时的M、N的位置,因为PQ、NM为定值,要想周长最小,则需要PM+NQ最小,即想办法做到一直线上,因此作P关于x轴的对称点P′,找到P′G=2,且P′G∥x轴,利用平移构建平行四边形P′GNM,从而得到x轴上的M和N,求出M的坐标.
解答 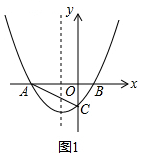 解:(1)如图1,把T(1,-$\frac{5}{4}$)代入抛物线y=$\frac{1}{a}$(x-2)(x+a)得:
解:(1)如图1,把T(1,-$\frac{5}{4}$)代入抛物线y=$\frac{1}{a}$(x-2)(x+a)得:
-$\frac{5}{4}$=$\frac{1}{a}$(1-2)(1+a),
解得:a=4,
∴抛物线的解析式为:y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2;
(2)当x=0时,y=$\frac{1}{a}$×(-2)×a=-2,
∴C(0,-2),
当y=0时,$\frac{1}{a}$(x-2)(x+a)=0,
x1=2,x2=-a,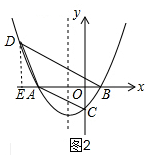
∴A(-a,0)、B(2,0),
如图2,过D作DE⊥x轴于E,
设D(m,n),
∵点D在第二象限,∠DAB为钝角,
∴分两种情况:
①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
∴tan∠BAC=tan∠ABD,即$\frac{OC}{OA}=\frac{DE}{BE}$,
∴$\frac{2}{a}=\frac{n}{-m+2}$,
n=$\frac{4-2m}{a}$,
则$\left\{\begin{array}{l}{n=\frac{4-2m}{a}}\\{n=\frac{1}{a}(m-2)(m+a)}\end{array}\right.$,
解得:m=-2-a或2,
∴E(-2-a,0),
由勾股定理得:AC=$\sqrt{{a}^{2}+4}$,
∵$\frac{AO}{AC}=\frac{BE}{BD}$,
∴$\frac{a}{\sqrt{{a}^{2}+4}}$=$\frac{-m+2}{BD}$=$\frac{a+4}{BD}$,
BD=$\frac{(a+4)\sqrt{{a}^{2}+4}}{a}$,
∵△BDA∽△ABC,
∴$\frac{AB}{BD}=\frac{AC}{AB}$,
∴AB2=AC•BD,
即(a+2)2=$\sqrt{{a}^{2}+4}$•$\frac{(a+4)\sqrt{{a}^{2}+4}}{a}$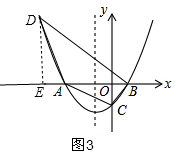 ,
,
解得:0=16,此方程无解;
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,
∵B(2,0),C(0,-2),
∴OB=OC=2,
∴△OBC是等腰直角三角形,
有BC=2$\sqrt{2}$,
∴∠OCB=∠OBC=45°,
∴∠ABC=∠ABD=45°,
∴DE=BE,
n=-m+2,
∴BD=$\sqrt{2{n}^{2}}$,
∵△DBA∽△ABC,
∴$\frac{BD}{AB}=\frac{AB}{BC}$,
∴AB2=BD•BC,
∴(a+2)2=$\sqrt{2{n}^{2}}$•2$\sqrt{2}$=4n,
则$\left\{\begin{array}{l}{(a+2)^{2}=4n}\\{n=-m+2}\\{n=\frac{1}{a}(m-2)(m+a)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-4\sqrt{2}-4}\\{n=6+4\sqrt{2}}\\{a=2+2\sqrt{2}}\end{array}\right.$,
则a=2+2$\sqrt{2}$;
(3)当x=6时,y=$\frac{1}{4}$(6-2)(6+4)=10,
∴Q(6,10),
如图4,作P关于x轴的对称点P′,过P′作P′G∥x轴,且P′G=2,连接GQ交x轴于N,过P′作P′M∥GN,交x轴于M,
此时,QG就是MP+NQ的最小值,由于PQ、NM为定值,所以此时,四边形PMNQ的周长最小,
∵P(-1,1),
∴P′(-1,-1),
∵P′G∥MN,P′M∥GN,
∴四边形P′GNM是平行四边形,
∴MN=P′G=2,NG=P′M=PM,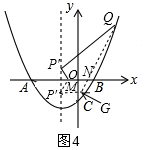
∴G(1,-1),
设GQ的解析式为:y=kx+b,
把G(1,-1)和Q(6,10)代入得:$\left\{\begin{array}{l}{k+b=-1}\\{6k+b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{11}{5}}\\{b=-\frac{16}{5}}\end{array}\right.$,
∴GQ的解析式为:y=$\frac{11}{5}$x-$\frac{16}{5}$,
当y=0时,x=$\frac{16}{11}$,
∴N($\frac{16}{11}$,0),
∵MN=2,
∴M(-$\frac{6}{11}$,0).
点评 本题是二次函数的综合题,考查了二次函数利用待定系数法求解析式及二次函数的性质,当两个三角形相似时,根据已知条件分类讨论;对于图形周长的最小值问题,要先确定哪此边是定值,哪些边是不确定值,根据轴对称的性质利用数形结合的思想解决问题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 普查就是全面地调查 | B. | 普查通过调查的方式来收集数据 | ||
| C. | 普查开展起来很方便 | D. | 普查的工作量大,消耗的时间长 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
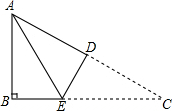 如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.
如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
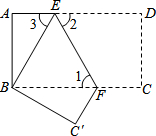 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com