
分析 首先化简$\frac{8}{{x}^{2}-4}$+$\frac{2}{x+2}$,然后把x=$\sqrt{5}$代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{8}{{x}^{2}-4}$+$\frac{2}{x+2}$
=$\frac{8}{{x}^{2}-4}$+$\frac{2x-4}{{x}^{2}-4}$
=$\frac{2x+4}{{x}^{2}-4}$
=$\frac{2}{x-2}$
当x=$\sqrt{5}$时,
原式=$\frac{2}{\sqrt{5}-2}$=2$\sqrt{5}$+4
点评 此题主要考查了分式的化简求值问题,要熟练掌握,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.


科目:初中数学 来源: 题型:填空题
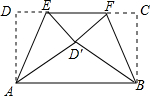 如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为$\frac{8}{3}$.
如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为$\frac{8}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
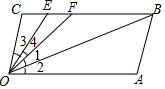 如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.
如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一三角形地块的四周种植宽度均为1m的草坪,外围三角均是以地块顶点为圆心的圆弧,并与各边通过相切连接,已知该三角形地块的周长为600m,则草坪外围的周长为(600+2π)m.
如图,在一三角形地块的四周种植宽度均为1m的草坪,外围三角均是以地块顶点为圆心的圆弧,并与各边通过相切连接,已知该三角形地块的周长为600m,则草坪外围的周长为(600+2π)m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(m,2$\sqrt{2}$),B(3$\sqrt{2}$,0),C(n,-2$\sqrt{2}$),AC经过原点O,BH⊥AC于H,则AC•BH的值为24.
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(m,2$\sqrt{2}$),B(3$\sqrt{2}$,0),C(n,-2$\sqrt{2}$),AC经过原点O,BH⊥AC于H,则AC•BH的值为24.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com