
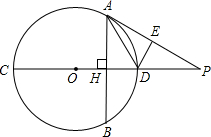
 如图,AB为⊙O内垂直于直径的弦,AB、CD相于点H,△AED与△AHD关于直线AD成轴对称.
如图,AB为⊙O内垂直于直径的弦,AB、CD相于点H,△AED与△AHD关于直线AD成轴对称.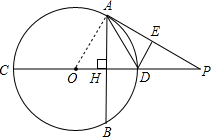 解:(1)连接OA.
解:(1)连接OA.| DP |
| PO |
| DE |
| AO |
| 1 |
| 2.5 |
| DE |
| 1.5 |
| 3 |
| 5 |


科目:初中数学 来源: 题型:
| 1 |
| 2 |

| 9 |
| 8 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 21、某数学学习小组想利用旗杆上的绳子测量校园内旗杆AB的高度(如图,AB垂直地面BC).方法如下:先把旗杆绳(AD)垂下,测得绳子底端D距地面刚好1m.然后拉住绳子底端向外走7步(每步距离约为0.6 m),刚好能拉住绳子底端放在一高为1.6 m的同学头顶上,求旗杆AB的长.
21、某数学学习小组想利用旗杆上的绳子测量校园内旗杆AB的高度(如图,AB垂直地面BC).方法如下:先把旗杆绳(AD)垂下,测得绳子底端D距地面刚好1m.然后拉住绳子底端向外走7步(每步距离约为0.6 m),刚好能拉住绳子底端放在一高为1.6 m的同学头顶上,求旗杆AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在同一平面内有A、B、C三个点,根据要求画图:
如图,在同一平面内有A、B、C三个点,根据要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
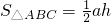 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.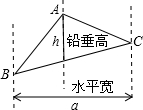
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.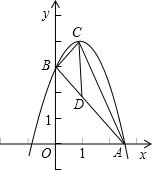
查看答案和解析>>
科目:初中数学 来源:2009-2010学年浙江省温州市永嘉县九年级(上)期末数学试卷(解析版) 题型:解答题
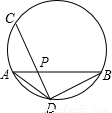
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
 S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com