
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
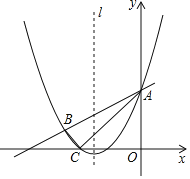
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)|MB﹣MC|取最大值为
;(2)|MB﹣MC|取最大值为![]() ;(3)存在点P(1,6),理由见解析
;(3)存在点P(1,6),理由见解析
【解析】
(1)①将A(0,3),C(3,0)代入y=![]() x2+bx+c,即可求解;
x2+bx+c,即可求解;
(2)分当点B、C、M三点不共线时、当点B、C、M三点共线时,两种情况分别求解即可;
(3)分当![]() 时、当
时、当![]() 时两种情况,分别求解即可.
时两种情况,分别求解即可.
(1)①将A(0,3),C(﹣3,0)代入y=![]() x2+bx+c得:
x2+bx+c得:
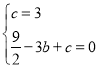 ,解得:
,解得:![]() ,
,
∴抛物线的解析式是![]() ;
;
(2)将直线y=![]() x+3表达式与二次函数表达式联立
x+3表达式与二次函数表达式联立
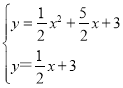
解得:x=0或﹣4,
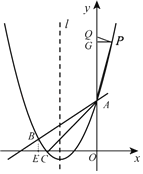
∵A (0,3),∴B(﹣4,1)
①当点B、C、M三点不共线时,
|MB﹣MC|<BC
②当点B、C、M三点共线时,
|MB﹣MC|=BC
∴当点、C、M三点共线时,|MB﹣MC|取最大值,即为BC的长,
过点B作x轴于点E,在Rt△BEC中,由勾股定理得BC=![]() =
=![]() ,
,
∴|MB﹣MC|取最大值为![]() ;
;
(3)存在点P使得以A、P、Q为顶点的三角形与△ABC相似.
设点P坐标为(x,![]() )(x>0)
)(x>0)
在Rt△BEC中,∵BE=CE=1,∴∠BCE=45°,
在Rt△ACO中,∵AO=CO=3,∴∠ACO=45°,
∴∠ACB=180°﹣450﹣450=900,AC=3![]() ,
,
过点P作PQ⊥PA于点P,则∠APQ=90°,
过点P作PQ⊥y轴于点G,∵∠PQA=∠APQ=90°
∠PAG=∠QAP,∴△PGA∽△QPA
∵∠PGA=∠ACB=90°
∴①当![]() 时,
时,
△PAG∽△BAC,
∴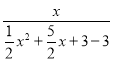 =
=![]() ,
,
解得x1=1,x2=0,(舍去)
∴点P的纵坐标为![]() ×12+
×12+![]() ×1+3=6,
×1+3=6,
∴点P为(1,6);
②当![]() 时,
时,
△PAG∽△ABC,
∴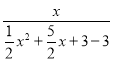 =3,
=3,
解得x1=﹣![]() (舍去),x2=0(舍去),
(舍去),x2=0(舍去),
∴此时无符合条件的点P
综上所述,存在点P(1,6).


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC 中,AB=AC.
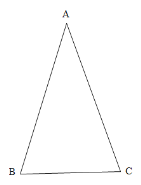
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
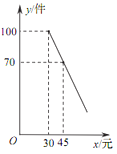
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ;
(2)抽查C厂家的合格零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家;
(4)若要从A、B、C、D四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用“列表法”或“画树形图”的方法求出(3)中两个厂家同时被选中的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
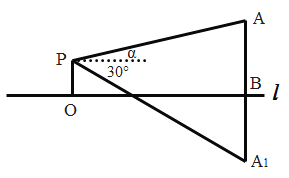
【题目】在湖心有一座小塔,小华想知道这座的高塔的高度,于是他在岸边架起了测角仪,他测量的数据如下(如图所示):测量仪位置![]() 距水平面
距水平面![]() 的距离为1.5米(即
的距离为1.5米(即![]() ),测得塔顶
),测得塔顶![]() 的仰角为
的仰角为![]() (其中
(其中![]() ),测得塔顶在水中倒影
),测得塔顶在水中倒影![]() (即
(即![]() )的俯角为
)的俯角为![]() ,请你根据上述数据求出这座塔的高度(即
,请你根据上述数据求出这座塔的高度(即![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com