
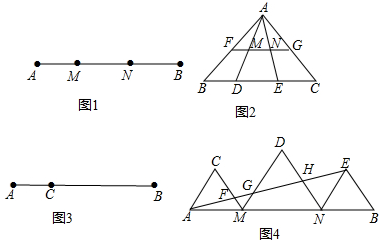
分析 (1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)先证出点M、N分别是AD、AE的中点,得出BD=2FM,DE=2MN,EC=2NG,求出EC2=BD2+DE2,得出NG2=FM2+MN2,即可得出结论;
(3)在AB上截取CE=CA;作AE点垂直平分线,截取CF=CA;作BF的垂直平分线,交AB于D即可;
(4)先证明△DGH≌△NEH,得出DG=EN=b,MG=c-b,再证明△AGM∽△AEN,得出比例式,得出c2=2ab-ac+bc,证出c2=a2+b2,得出a=b,证出△DGH≌△CAF,得出S△DGH=S△CAF,证出S△DMN=S△ACM+S△ENB,即可得出结论.
解答 (1)解:①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}-A{M}^{2}}$=$\sqrt{9-4}$=$\sqrt{5}$;
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}+A{M}^{2}}$=$\sqrt{9+4}$=$\sqrt{13}$,
综上所述:BN=$\sqrt{5}$或$\sqrt{13}$;
(2)证明:∵FG是△ABC的中位线,
∴FG∥BC,
∴$\frac{AM}{MD}$=$\frac{AN}{NE}$=$\frac{AG}{GC}$=1,
∴点M、N分别是AD、AE的中点,
∴BD=2FM,DE=2MN,EC=2NG,
∵点D、E是线段BC的勾股分割点,且EC>DE≥BD,
∴EC2=BD2+DE2,
∴(2NG)2=(2FM)2+(2MN)2,
∴NG2=FM2+MN2,
∴点M、N是线段FG的勾股分割点;
(3)解:作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图所示:
(4)解:S四边形MNHG=S△AMF+S△BEN,理由如下:
设AM=a,BN=b,MN=c,
∵H是DN的中点,
∴DH=HN=$\frac{1}{2}$c,
∵△MND、△BNE均为等边三角形,
∴∠D=∠DNE=60°,
在△DGH和△NEH中,
$\left\{\begin{array}{l}{∠D=∠DNE}\\{DH=HN}\\{∠DHG=∠NHE}\end{array}\right.$,
∴△DGH≌△NEH(ASA),
∴DG=EN=b,
∴MG=c-b,
∵GM∥EN,
∴△AGM∽△AEN,
∴$\frac{c-b}{b}=\frac{a}{a+c}$,
∴c2=2ab-ac+bc,
∵点 M、N是线段AB的勾股分割点,
∴c2=a2+b2,
∴(a-b)2=(b-a)c,
又∵b-a≠c,
∴a=b,
在△DGH和△CAF中,
$\left\{\begin{array}{l}{∠D=∠C}\\{DG=CA}\\{∠DGH=∠CAF}\end{array}\right.$,
∴△DGH≌△CAF(ASA),
∴S△DGH=S△CAF,
∵c2=a2+b2,
∴$\frac{\sqrt{3}}{4}$c2=$\frac{\sqrt{3}}{4}$a2+$\frac{\sqrt{3}}{4}$b2,
∴S△DMN=S△ACM+S△ENB,
∵S△DMN=S△DGH+S四边形MNHG,S△ACM=S△CAF+S△AMF,
∴S四边形MNHG=S△AMF+S△BEN.
点评 本题是相似形综合题目,考查了新定义“勾股分割点”、勾股定理、三角形中位线定理、全等三角形的判定与性质、相似三角形的判定与性质、等边三角形的性质、三角形和四边形面积的计算等知识;本题难度较大,综合性强,特别是(4)中,需要两次证明三角形全等和三角形相似才能得出结论.


科目:初中数学 来源: 题型:解答题
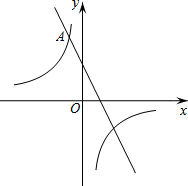 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )| A. | 10 | B. | $\sqrt{7}$ | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
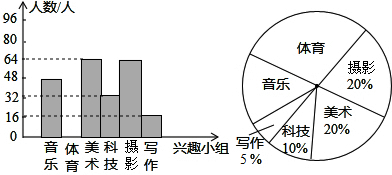
| A. | 七年级共有320人参加了兴趣小组 | |
| B. | 体育兴趣小组对应扇形圆心角的度数为96° | |
| C. | 各小组人数组成的数据的众数是64 | |
| D. | 各小组人数组成的数据的中位数是56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com