
【题目】已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x-h)2+k的形式;
(2)用五点法画出此函数图象的示意图.
【答案】(1)y=-(x-2)2+1.(2)画图见解析.
【解析】
试题(1)先将点(﹣1,﹣8),(0,﹣3)代入y=﹣x2+bx+c,列出关于b、c的二元一次方程组,求解得出b、c的值,得到二次函数的表达式,再用配方法化为顶点式的形式
(2)利用描点法画出函数图象即可.
解:(1)∵二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3),
∴![]() ,解得
,解得![]() ,
,
∴此二次函数的表达式为y=﹣x2+4x﹣3;
y=﹣x2+4x﹣3=﹣(x﹣2)2+1;
(2)∵y=﹣(x﹣2)2+1,
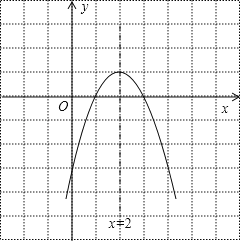
∴顶点坐标为(2,1),对称轴方程为x=2.
∵函数二次函数y=﹣x2+4x﹣3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为


科目:初中数学 来源: 题型:
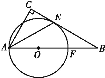
【题目】如图,在Rt△ABC中,∠C=90°,O是AB上一点, ⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
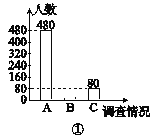
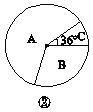
【题目】为了了解初中生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:A.只愿意就读普通高中;B.只愿意就读中等职业技术学校;C.就读普通高中或中等职业技术学校都愿意.学校教务处将调查数据进行了整理,并绘制了如图25-3-3所示的尚不完整的统计图,请根据相关信息,解答下列问题:
(1)本次活动共调查了多少名学生?
(2)补全图①,并求出图②中B区域的圆心角的度数;
(3)若该校八、九年级的学生共有2800名,请估计该校八、九年级学生中只愿意就读中等职业技术学校的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
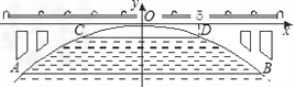
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠B=∠C,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
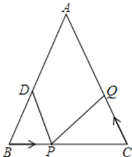
(1)用含t的式子表示PC的长为 ;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示1,现将点
表示1,现将点![]() 沿
沿![]() 轴做如下移动,第一次点
轴做如下移动,第一次点![]() 向左移动3个单位长度到达点
向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是__________.
的最小值是__________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com