
分析 首先根据图象经过点A(-6,0),可得0=-6k+b,进而得到b=6k,再根据△AOB的面积为12可得:$\frac{1}{2}$AO•OB=12,进而可得$\frac{1}{2}$•6•|b|=12,算出|b|的值,再计算出b,然后把b的值代入b=6k即可算出答案.
解答 解:∵图象经过点A(-6,0),
∴0=-6k+b,
即b=6k ①,
∵图象与y轴的交点是B(0,b),
∴$\frac{1}{2}$AO•OB=12,
即:$\frac{1}{2}$•6•|b|=12,
∴|b|=4,
∴b1=4,b2=-4,
代入①式,得k1=$\frac{2}{3}$,k2=-$\frac{2}{3}$,
一次函数的表达式是y=$\frac{2}{3}$x+4或y=-$\frac{2}{3}$x-4.
点评 此题主要考查了求一次函数解析式,关键计算出|b|的值,注意b有两个值,不要片面的得到一个值.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
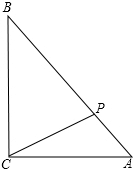 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com