
【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
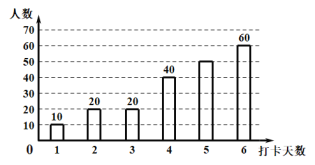
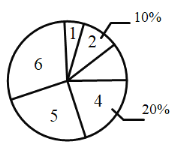
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
【答案】(1) ![]() ,
,![]() ,补全图形如下所示;(2) 900人;(3) 5天.
,补全图形如下所示;(2) 900人;(3) 5天.
【解析】
(1)通过扇形统计图中打卡天数为4天时所占的比例为20%,求出总人数,然后再减去打卡天数分别为1/2/3/4/6天的人数,即得到打卡天数为5天的人;然后再按打卡天数从小到大排列,最中间的打卡天数得出中位数a的值,出现次数最多的即为众数,求出b的值.
(2)算出打卡天数大于等于4天的人数的占比,然后再用1200乘以这个占比,即得到体育锻炼合格的人数.
(3)设漏掉的这名学生坚持打卡天数最少是x天,然后将新的平均数用x的代数式表示,其大于4.4天,进而得到不等式,求出x的最少天数.
解:(1)由题意,设打卡天数为4天的占20%,
故总人数为:40÷20%=200人
∴打卡天数为5天的人为:200-10-20-20-40-60=50人
故补全条形统计图如下所示:
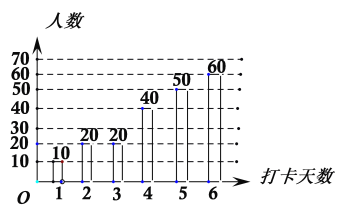
总共200人,按从小到大排列最中间的两位数为100和101,第100和101名同学对应的打卡天数均是5天,故中位数是5,∴![]()
众数是出现次数最多的数,∴![]()
故答案为:![]() ,
,![]() .
.
(2) 打卡天数大于等于4天的人数有:40+50+60=150人
其占200人的比重为:150÷200×100%=75%
故![]() 人中体育锻炼合格的人数为:1200×75%=900人
人中体育锻炼合格的人数为:1200×75%=900人
故答案为:900人体育锻炼合格.
(3) 设漏掉的这名学生坚持打卡天数最少是x天,将漏掉的学生加入后,
新的打卡天数的平均数大于4,故由:
![]()
解不等式得:![]()
又锻炼天数x为整数,∴![]()
故答案为:这名学生坚持打卡天数最少是5天.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象和
的图象和![]() 都在第一象限内,
都在第一象限内,![]() ,
,![]() 轴,且
轴,且![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)若反比例函数![]() 的图象经过点B,求此反比例函数的解析式;
的图象经过点B,求此反比例函数的解析式;
(2)若将![]() 向下平移
向下平移![]() (m>0)个单位长度,
(m>0)个单位长度,![]() ,
,![]() 两点的对应点同时落在反比例函数图象上,求
两点的对应点同时落在反比例函数图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降![]() 元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当
元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当![]() 为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
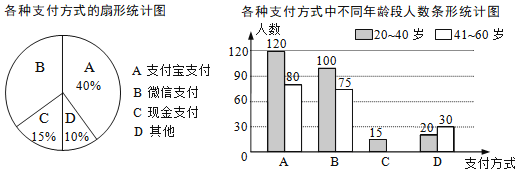
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和点
和点![]() 给出如下定义:若
给出如下定义:若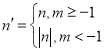 ,则称点
,则称点![]() 为点
为点![]() 的绝对点.例如:点
的绝对点.例如:点![]() 的绝对点坐标是
的绝对点坐标是![]() ,点
,点![]() 的绝对点坐标是
的绝对点坐标是![]() .
.
(1)点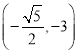 的绝对点坐标是_______.
的绝对点坐标是_______.
(2)若点![]() 在函数
在函数![]()
![]() 的图像上,其绝对点
的图像上,其绝对点![]() 的纵坐标
的纵坐标![]() 的取值范围为
的取值范围为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若点![]() 在关于
在关于![]() 的二次函数
的二次函数![]() 图像上,其绝对点
图像上,其绝对点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() 或
或![]() ,其中
,其中![]() ,令
,令![]() ,是否存在
,是否存在![]() 使得
使得![]() 有最大值,若有请求出
有最大值,若有请求出![]() 的最大值及此时
的最大值及此时![]() 的值;若无,请说明理由.
的值;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+c的顶点为P(1,9),与x轴的交点为A(﹣2,0),B.
(1)求抛物线的解析式;
(2)M为x轴上方抛物线上的一点,MB与抛物线的对称轴交于点C,若∠COB=2∠CBO,求点M的坐标;
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为y=ax2+bx+h,E,F新抛物线在第一象限内互不重合的两点,EG⊥x轴,FH⊥x轴,垂足分别为G,H,若始终存在这样的点E,F,满足△GEO≌△HOF,求h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③3是方程ax2+2x+c=0的一个根;
④当﹣1<x<3时,ax2+2x+c>0
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
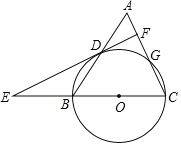
【题目】如图,在三角形ABC中,AB=10,AC=BC=13,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF⊥AC,于点F,交CB的延长线于点E.
(1)求证:DF是⊙O的切线;
(2)求cos∠ADF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com